1、SFT 和 PEFT

SFT（Supervised Fine-Tuning，监督微调）是针对大规模语言模型（LLM）进行二次训练的一个重要步骤。在预训练阶段，LLM 通常通过大量的无标签数据进行训练，以掌握语言的基本结构和知识。然而，预训练模型往往缺乏针对特定任务的深度优化，这时就需要通过 SFT 来进一步提升模型在特定任务或应用中的性能。

PEFT（Parameter-Efficient Fine-Tuning，参数高效微调）是一种针对大规模预训练语言模型（LLM）进行微调的技术，它旨在通过尽量减少更新的参数量来提高微调效率，同时尽可能保持模型的性能。与全参数微调（Full Fine-Tuning，监督微调）不同，PEFT 通过降低微调过程中所需的参数数量来减轻计算和存储的负担，使得微调更具高效性，特别适合应用于资源受限的场景。

2、LLM 计算流程

以 LLaMA 为例，本节分析 LLM 计算流程，包括其基本组件、计算复杂度以及它所涉及的计算流程。

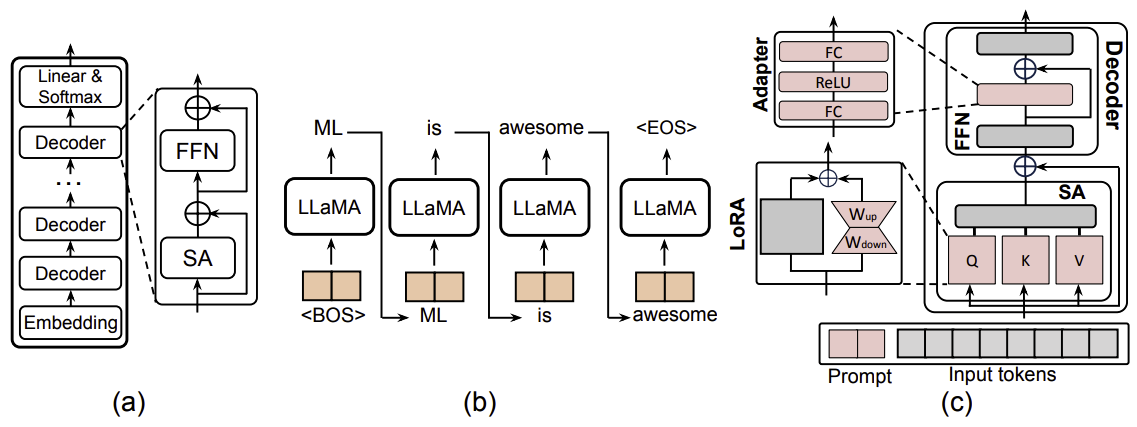
如图中（a）所示，LLaMA 由三个主要部分组成：一个嵌入模块、一组堆叠的解码器模块，以及一个由线性层和 Softmax 层构成的头部模块。

嵌入层的主要作用是将无结构的文本信息转换为离散的数值向量块（tokens），以便于后续处理。然后，这些 embedded tokens 会被传送到解码器层进行进一步处理。每个 LLaMA 解码器由两个基本组件构成：多头自注意力机制（MSA）和前馈网络（FFN）。在多头自注意力机制模块中，每个标记会通过输入标记的两个线性映射之间的点积所得到的注意力图进行聚类。然后，这些成组的标记会由前馈神经网络进一步处理。此外，LLaMA 中采用了均方根层归一化（RMSNorm）来替代层归一化，以确保高效的训练过程。

LLM 具有内在的自回归特性，这就需要多次迭代才能完成生成任务。此外，LLM 融入了注意力机制，这是一个计算复杂度会随着输入长度呈二次方增长的组件。另一方面，LLM 的内在计算特性在于每个解码器层中的注意力模块。图中（c）展示了注意力模块中计算流程的总体概览。

在推理过程中，每个解码器将一个三维张量 $x \in \mathbb{R}^{b \times l \times d}$ 作为输入标记。输入标记首先会与三个权重矩阵 $W_Q$ 、 $W_K$ 和 $W_V$ 相乘，产生被称为查询（ $Q$ ）、键（ $K$ ）和值（ $V$ ）的输出。鉴于多头自注意力机制模块无法识别位置数据，且大语言模型具有内在的自回归特性，Query 和 Key 将通过旋转位置嵌入（RoPE，在如下公式（1）中表示为 $R_p(q)$ ）进行一个处理过程，以对位置信息进行编码。随后，Key 和 Value 将与先前的标记相结合。

在位置嵌入之后，中间激活值将经历一系列的乘法、Softmax 运算以及残差相加操作，以生成如公式（9）中所描述的多头自注意力机制输出。在此需要注意的是，公式中的 $d_k$ 指的是多头注意力机制中的特征维度数量。

\[Q, K, V = R(W_q x), R(W_k x), W_v x \tag{1}\] \[SA(x) = \operatorname{Softmax}\left(\frac{Q K^T}{\sqrt{d_{\text{head}}}}\right) V \tag{2}\] \[MSA(x) = \left[SA_1(x); SA_2(x); \ldots; SA_k(x)\right] W_o \tag{3}\]

SA 输出将被转发到 FFN 块进行进一步处理。FFN 块将有另外三个矩阵 $W_{up}$、$W_{down}$ 和 $W_{gate}$，并且计算可以表示为：

\[FFN_{LLaMA}(x) = W_{up}(\operatorname{SiLU}(W_{\text{gate}} x) \odot (W_{\text{down}} x)) + x, \tag{4}\]

其中 $x$ 表示 FFN 层的输入，SiLU 是 LLaMA 中使用的非线性函数。在原始 Transformer 中，FFN 块可以表示为：

\[FFN_{\text{Transformer}}(x) = W_{up}(\operatorname{ReLU}(W_{\text{down}} x)) + x. \tag{5}\]

最后一个解码器层的输出将被送至一个线性层，该线性层随后会生成一个覆盖整个词汇表的概率分布，以此来预测序列中的下一个标记。生成的标记会与之前的标记拼接在一起，并作为下一轮处理的输入。这个生成过程会以自回归的方式不断重复，直至生成一整个标记序列，即一个完整结果（图（b））。

在训练过程中，计算流程与推理过程类似，不同之处在于，会将生成的句子直接与真实输出进行比较，并计算训练损失。然后，会在大语言模型的权重上计算梯度，以最小化这个训练损失。

大语言模型每次生成一个标记（单词），其生成过程基于之前的提示（输入）和先前已生成的序列。这个过程会不断重复，直到模型输出终止标记。为了加速大语言模型的推理过程，采用将先前的键（Keys）和值（Values）存储在键值缓存（KV-cache）中的策略，这样就无需为每个新标记重新计算它们。从数学角度，可以用公式（6）来表示所有解码器的键值缓存内存成本：

\[Size = L \times 2 \times b \times l \times d_{head} \times n_{head} \tag{6}\]

其中，$l$ 表示上下文长度，$b$ 表示批量大小，$L$ 表示层数，$d_{head}$ 表示头维度，$n_{head}$ 表示头的数量。

3、PEFT 分类

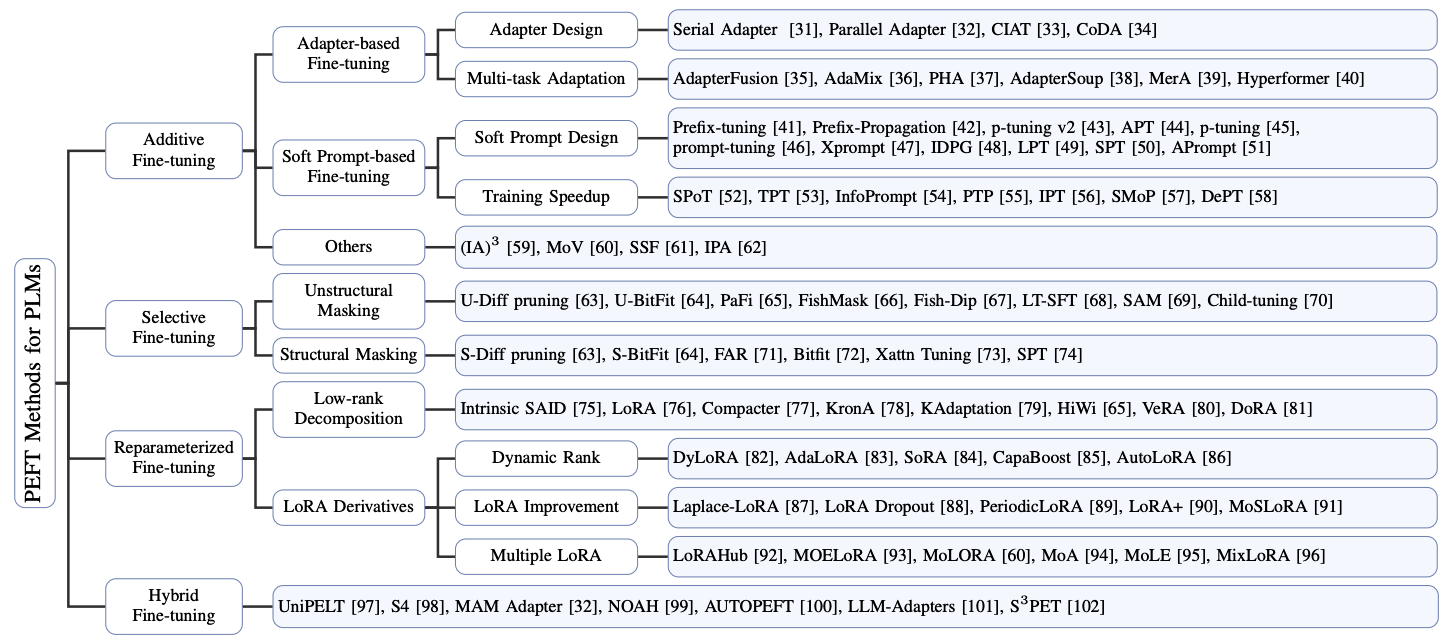
参数高效微调（PEFT）策略大致可分为四类：

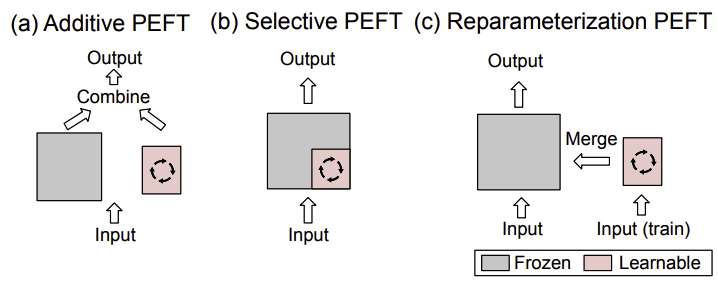
• additive PEFT： 通过注入新的可训练模块或参数来修改模型架构
• selective PEFT： 在微调过程中使一部分参数子集变为可训练的
• reparameterized PEFT： 构建原始模型参数的（低维）重新参数化形式用于训练，然后在推理时将其等效转换回原始形式
• hybrid PEFT： 结合不同参数高效微调方法的优点来构建一个统一的参数高效微调模型

3.1、Additive PEFT

标准的全量微调需要大量的计算开销，并且还可能潜在地损害模型的泛化能力。为了缓解这个问题，一种广泛采用的方法是保持预训练的主干模型不变，仅引入最少量的可训练参数，这些参数被策略性地放置在模型架构中。在针对特定的下游任务进行微调时，仅更新这些额外模块或参数的权重，使得存储、内存和计算资源需求大幅减少。由于这些技术具有添加参数的特点，因此可以将其称为 additive PEFT。

3.1.1、适配器

适配器（Adapters）方法是在 Transformer 模块中插入小型的适配器层。通常，一个适配器层由一个下投影矩阵 $W_{down} \in \mathbb{R}^{r\times d}$、一个非线性激活函数 $\sigma(\cdot)$ 和一个上投影矩阵 $W_{up} \in \mathbb{R}^{d\times r}$ 组成。其中，$d$ 表示隐藏层的维度，$r$ 是瓶颈维度，用于配置适配器的一个超参数。将 $h_{in}$ 记为适配器的输入，适配器模块（带有残差连接）内的计算可以总结如下：

\[Adapter(x) = W_{up}\sigma(W_{down}x) + x \tag{7}\]

自然语言处理（NLP）领域中适配器的概念最初由串行适配器（Serial Adapter）提出，如下图中（a）所示。每个 Transformer 模块通过添加两个适配器模块得到增强，一个位于自注意力层之后，另一个位于前馈网络（FFN）层之后。后续的研究旨在解决适配器层带来的额外计算成本问题。于是提出了一种改进框架——AdapterFusion，在该框架中，适配器层仅被插入到 FFN 层之后的 “Add & Norm” 步骤之后，以提高计算效率。

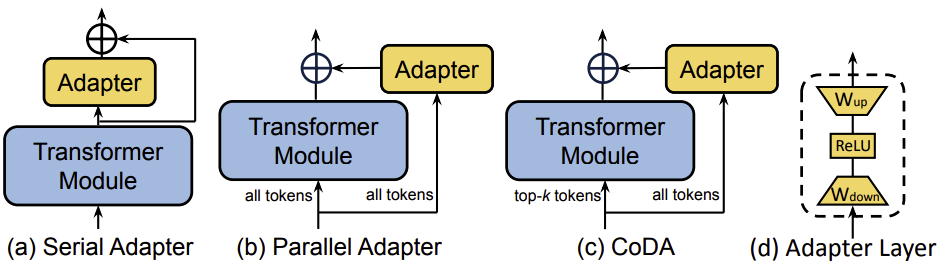
上述适配器采用的是顺序设计，将适配器层作为瓶颈放置在 Transformer 模块内。这种方法可能会降低模型的并行性，需要在推理效率和准确性之间进行权衡。相比之下，一种并行适配器（PA）方法，如图中（b）所示，将传统的顺序适配器层重新组织成一个与每个 Transformer 子层并行运行的侧网络。同样，CIAT、CoDA 和 KronA 也采用了并行适配器设计。除了并行设计之外，CoDA 采用了一种稀疏激活机制来提高推理效率，如图中（c）所示。具体来说，CoDA 使用一种 soft top-k 选择过程，识别出每一层中的 $k$ 个重要标记，这些标记将由冻结的预训练 Transformer 层和适配器分支共同处理，以保持模型的准确性。相反，那些不重要的标记仅由适配器分支处理，跳过繁重的预训练层，从而在不影响整体性能的前提下优化推理效率。

为了提高适配器的性能和泛化能力，各种研究都实施了多任务学习策略，例如 AdapterFusion、AdaMix、PHA、AdapterSoup、MerA 和 Hyperformer。适配器融合将所有预训练的适配器保留在模型中，并使用一个融合模块来合并多任务信息。与适配器融合不同，MerA 通过基于权重和激活的最优传输将预训练的适配器合并为一个。这种方法避免引入任何额外的可训练参数，从而提高了计算效率。超变换器将多任务信息存储在一个共享的超网络中，该超网络根据任务和层的 ID 嵌入生成特定于任务和层的适配器参数。对于一个新任务，只需要学习一个额外的任务嵌入，因此减少了需要训练的参数数量。

Serial Adapter Tuning

适配器是添加到预训练网络各层之间的新模块。基于适配器的调优与基于特征的迁移学习和微调有以下区别。

考虑一个带有参数 $w$ 的函数（神经网络）：$\varphi_w(x)$。基于特征的迁移学习将 $\varphi_w$ 与一个新函数 $\chi_v$ 组合，得到 $\chi_v(\varphi_w(x))$。然后，仅对新的、特定于任务的参数 $v$ 进行训练。微调则是针对每个新任务调整原始参数 $w$，这限制了模型的紧凑性。

对于适配器调优，定义了一个新函数 $\psi_{w,v}(x)$，其中参数 $w$ 是从预训练阶段复制过来的。初始参数 $v_0$ 的设置要使得新函数近似于原始函数：$\psi_{w,v_0}(x) \approx \varphi_w(x)$。在训练过程中，仅对 $v$ 进行调优。

对于深度网络，定义 $\psi_{w,v}$ 通常需要在原始网络 $\varphi_w$ 中添加新的层。如果选择 $|v| \ll |w|$，那么对于许多任务，得到的模型大约需要 $|w|$ 个参数。由于 $w$ 是固定的，该模型可以扩展到新任务，而不会影响之前的任务。

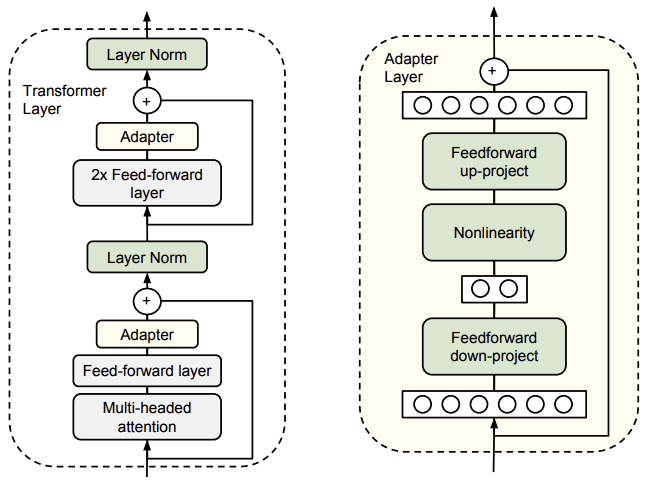
下图展示了适配器架构及其在 Transformer 中的应用。Transformer 的每一层包含两个主要的子层：注意力层和前馈层。这两个层之后都会紧接着进行一次投影操作，将特征维度映射回该层输入的维度大小。每个子层都应用了跳跃连接。每个子层的输出会被输入到层归一化操作中。

Adapter Tuning 在每个子层之后插入两个串行的适配器。适配器总是直接应用于子层的输出，即在投影回输入维度大小之后，但在添加跳跃连接之前。然后，适配器的输出会直接传递到后续的层归一化操作中。

为了限制参数数量，Adapter Tuning 提出了一种瓶颈架构。适配器首先将原始的 $d$ 维特征投影到一个较小的维度 $m$，应用一个非线性激活函数，然后再投影回 $d$ 维。每层添加的参数总数（包括偏置项）为 $2md + d + m$。通过设置 $m$ 远小于 $d$，限制了每个任务添加的参数数量。

在实践中，使用的参数数量约为原始模型参数的 $0.5 - 8 \%$。瓶颈维度 $m$ 提供了一种在性能和参数效率之间进行权衡的简单方法。适配器模块本身内部也有一个跳跃连接。有了这个跳跃连接，如果投影层的参数初始化为接近零，那么该模块会被初始化为一个近似的恒等函数。

左侧：在每个 Transformer 层中添加两次适配器模块，一次是在多头注意力机制后的投影操作之后，另一次是在两个前馈层之后。

右侧：适配器包含一个瓶颈层，与原始模型中的注意力层和前馈层相比，该瓶颈层的参数较少。适配器还包含一条跳跃连接。在适配器调优过程中，绿色的层会在下游数据上进行训练，这些层包括适配器、层归一化参数以及最终的分类层（图中未显示）。

3.1.2、Soft Prompt

Prompt Tuning 是一种通过微调来改进模型性能的方法。与通过上下文学习优化离散的词元表示不同，人们普遍认为 soft prompts 的连续嵌入空间本身包含更多信息。受此启发，研究人员直接将可调整的向量（即 soft prompts）添加到输入序列的开头。可以表示为：

\[X^{(l)} = [s^{(l)}_1, ..., s^{(l)}_{N_S}, x^{(l)}_1, ..., x^{(l)}_{N_X}] \tag{8}\]

其中，$X^{(l)}$ 是第 $l$ 层的输入词元序列，包括 soft prompt 词元 $s^{(l)}_i$ 以及随后的原始输入词元 $x^{(l)}_i$。$N_S$ 是 soft prompt 的数量，$N_X$ 是原始输入词元的数量。

Prefix-tuning 引入了可学习的向量，并将其添加到所有 Transformer 层的键（$k$）和值（$v$）之前。为了确保优化过程的稳定性，前缀调优采用了重参数化（reparameterization）策略，即使用一个多层感知机（MLP）层来生成这些前缀向量，而不是直接对其进行优化。微调完成后，推理时仅保存前缀向量。这项技术在多项研究中得到了调整和改进。例如，p-tuning v2 去除了重参数化步骤，并将其应用范围扩展到更大规模的模型和更多的自然语言处理任务。

APT（Adaptive Prefix Tuning）通过引入自适应门控机制来控制每层中前缀的重要性，从而增强了前缀调优的效果。同期的工作 p-tuning 和 prompt-tuning 仅在初始词嵌入层应用可学习的向量，而非在所有层应用，以提高训练和推理效率。值得强调的是，提示调优主要在大型模型（特别是参数超过 110 亿的模型）中表现出有效性。与之互补的是，Xprompt 通过分层结构的剪枝去除了负向提示词元，缩小了小模型规模下的性能差距。

基于实例的提示生成（IDPG，Instance-Dependent Prompt Generation）通过一个轻量级的提示生成器为每个输入句子生成提示，从而改进了提示调优。与之相关的后期提示调优（LPT，Late Prompt Tuning）同样利用提示生成器来获取与实例相关的提示。与以往的工作不同，LPT 仅在中间层之后添加这些提示，而非在初始层或所有层添加。这种策略性的放置方式消除了中间层以下的梯度计算，从而显著加快了训练速度。同时，由于较短的反向传播路径保留了更多与任务相关的信息，LPT 还能提高整体性能。

受 LPT 的启发，选择性提示调优（SPT，Selective Prompt Tuning）进一步深入研究了提示插入策略的重要性。它在每层引入了一个可学习的概率门，以确定是使用从上一层传播而来的提示，还是注入一个新生成的提示。

APrompt 采用了另一种提示插入策略。除了在每个 Transformer 层的输入序列开头插入输入提示外，APrompt 还在自注意力块的查询、键和值矩阵前分别添加额外的可学习提示，以学习新的注意力模式。此外，APrompt 还包含特定任务头部的学习。

soft prompts 的概念已被应用于各种下游任务，尽管其训练过程容易出现不稳定和收敛速度慢的问题。为了解决这些问题，提示转移（SPoT，Source Prompt Transfer）使用从一个或多个任务中学到的源提示来初始化新任务的提示。

类似地，可迁移提示调优（TPT，Transferable Prompt Tuning）提出将 soft prompt 从一个任务迁移到另一个任务进行初始化，结果表明更好的提示初始化可以大幅加快训练收敛速度。

信息提示（InfoPrompt）开发了两个基于互信息的损失函数，即头部损失和表示损失，以找到更好的提示初始化并学习足够的与任务相关的信息，从而也加快了收敛速度。

提示调优稳定性改进（PTP，Prompt Tuning with Perturbation）深入研究了训练不稳定的根本原因。它发现传统提示调优的损失曲面很陡峭，输入数据的微小变化可能导致损失大幅波动。为了缓解这一问题，PTP 引入了基于扰动的正则化项来平滑损失曲面，从而稳定训练过程。

分解提示调优（DePT，Decomposed Prompt Tuning）将 soft prompts 分解为一个较短的 soft prompts 和一对低秩矩阵，并以两种不同的学习率对它们进行优化。这种策略不仅提高了性能，还增强了训练和推理效率。

稀疏提示混合（SMoP，Sparse Mixture-of-Prompts）通过使用短 soft prompt 降低了训练和推理成本。在训练过程中，训练多个短 soft prompt，每个短 soft prompt 针对数据集的特定子集。在推理过程中，SMoP 集成了一个门控机制，将每个输入实例路由到合适的短提示。这种技术不仅提高了训练和推理阶段的效率，还能保持与使用较长 soft prompt 相当的性能。

为了进一步减少 soft prompt 参数的数量，内在提示调优（IPT，Intrinsic Prompt Tuning）通过在多个任务上训练自编码器来识别内在任务子空间。在新任务上进行调优时，只需调整该子空间内的几个参数，从而显著减少了训练参数的数量。

Prefix Tuning

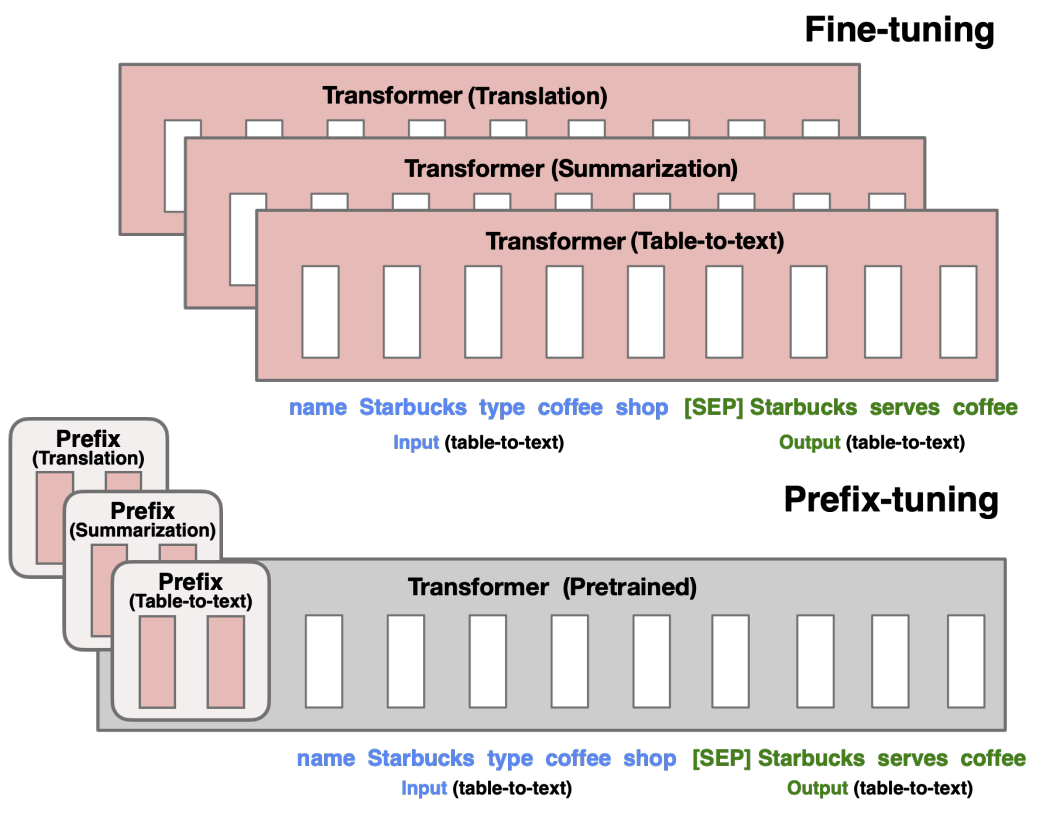
如图，微调会更新语言模型（LM）的所有参数（红色的 Transformer 模块），并且针对每个任务都需要存储完整的模型副本。Prefix Tuning 提出了前缀调优方法，该方法冻结语言模型的参数，仅对前缀（红色的前缀块）进行优化。因此，针对每个任务只需存储前缀，这使得前缀调优具有模块化特性且节省空间。（注：每个垂直块表示一个时间步的 Transformer 激活值）

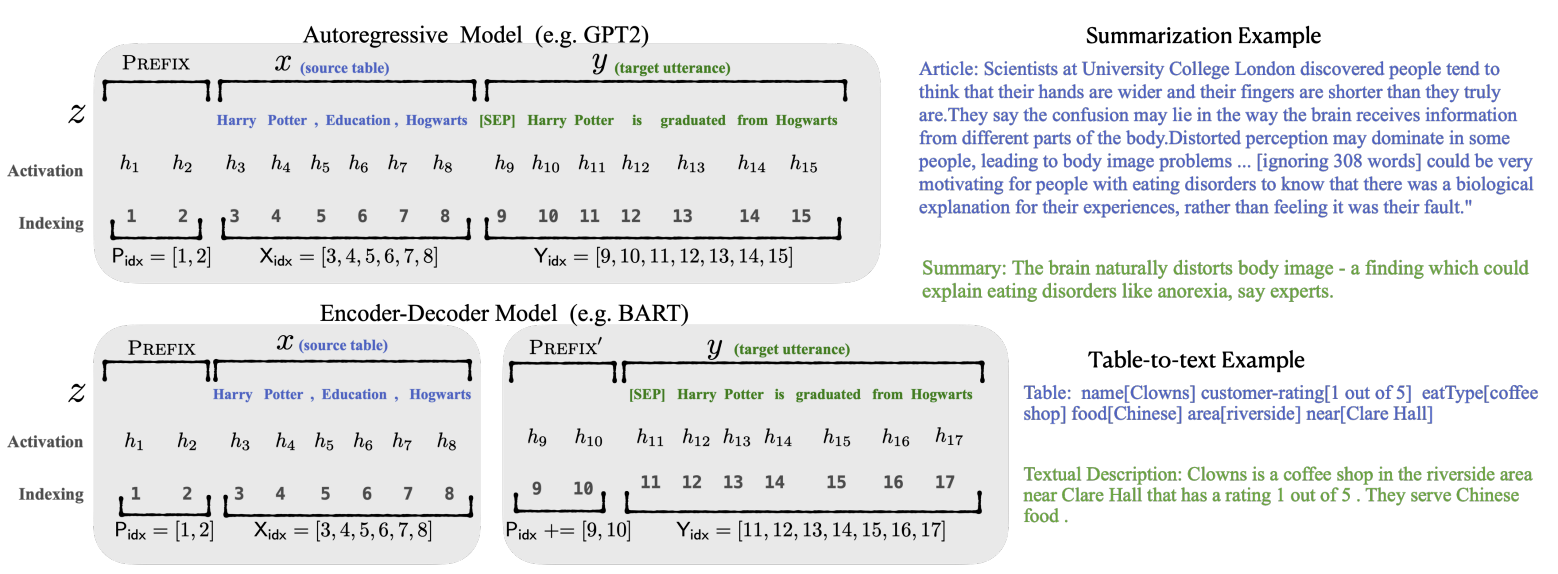
前缀调优是指为自回归语言模型（Autoregressive Language Model，LM）添加一个前缀，得到 $z = [前缀; x; y]$ ；或者为编码器和解码器都添加前缀，得到 $z = [前缀; x; 前缀’; y]$ ，如下图所示。这里，$P_{idx}$ 表示前缀索引序列，用 $|P_{idx}|$ 表示前缀的长度。

前缀索引对应的激活值是自由参数，这些自由参数由一个维度为 $|P_{idx}| \times \text{dim}(h_i)$ 的矩阵 $P_{\theta}$（由 $\theta$ 参数化）给出。

\[h_i = \begin{cases} P_{\theta}[i, :], & \text{如果 } i \in P_{idx} \\ \text{LM}_{\varphi}(z_i, h_{<i}), & \text{否则 } \end{cases}\]

其中，语言模型的参数 $\varphi$ 被固定，只有前缀参数 $\theta$ 是可训练参数。每个 $h_i$ 都是可训练矩阵 $P_{\theta}$ 的函数。当 $i \in P_{idx}$ 时，$h_i$ 直接从 $P_{\theta}$ 复制；当 $i \notin P_{idx}$ 时，$h_i$ 仍然依赖于 $P_{\theta}$ ，因为前缀激活值始终处于左侧上下文，因此会影响右侧的任何激活值。

从经验来看，直接更新 \(P_{\theta}\) 参数会导致优化过程不稳定，并且性能会略有下降。所以，Prefix Tuning 通过一个较小的矩阵 \((P'_{\theta})\) 与一个大型前馈神经网络（\(MLP_{\theta}\)）的组合来对矩阵 \(P_{\theta}[i, :]\) 进行重新参数化，即 \(P_{\theta}[i, :] = MLP_{\theta}(P'_{\theta}[i, :])\)。

现在，可训练参数包括 \(P'_{\theta}\) 和 \(MLP_{\theta}\) 的参数。请注意，\(P_{\theta}\) 和 \(P'_{\theta}\) 的行数相同（即前缀长度相同），但列数不同。

一旦训练完成，这些 MLP 中的重新参数化的参数可以被丢弃，只需要保存前缀 $(P_{\theta})$ 。

P-Tuning

大模型的 Prompt 构造方式对下游任务效果有显著影响。比如，GPT-3 使用人工构造的模板进行上下文学习（in-context learning），但模板的变化极其敏感，哪怕是增加、删除或调整词语位置，都会引起较大波动。

当对语言模型进行微调时，不稳定性问题会有所缓解，但不同提示之间的性能差异仍然相当大，尤其是在小样本设置下。近来的自动提示方法试图针对给定任务搜索性能更优的提示，但这些方法并未改变离散提示不稳定的本质。

P-Tuning 的核心创新在于将传统离散提示（Discrete Prompt）转化为可学习的连续嵌入层（Embedding Layer），该方法在优化过程中面临两个关键挑战：

• 离散性
  • 预训练模型的提示编码器已通过海量数据固化语义表征能力（高度离散），若直接采用随机初始化的提示嵌入进行端到端训练，会导致两个问题：
    • 提示向量与冻结的预训练参数存在表征空间错位
    • 梯度优化易陷入局部最优，难以收敛到有意义的语义空间
• 相关性
  • 随机初始化的提示向量缺乏预设的语义关联，而语言模型的生成效果依赖于提示间的逻辑连贯性。离散提示通过人工设计保证语义关联（如”[X]的答案是[Y]”），但连续嵌入的随机性会破坏这种关联结构，导致模型难以捕捉有效的推理路径

P-Tuning 将可训练的连续提示嵌入（continuous prompt embeddings）与离散提示（discrete prompt）相结合使用。具体而言，给定一个离散提示作为输入，P-Tuning 将连续提示嵌入与离散提示词元拼接起来，并将其作为输入送入语言模型。连续提示通过反向传播进行更新，以优化任务目标。

其背后的直觉是，连续提示为输入引入了一定程度的可学习性，这可能会学习抵消离散提示中微小变化的影响，从而提高训练稳定性。

形式上，设 $M$ 是一个预训练语言模型，其隐藏层维度为 $h$，词汇表大小为 \(\\|V\\|\)。 设 \(\{(x_i, y_i)\}_i\) 是一个用于自然语言理解（NLU）任务的标注数据集，其中 \(x_{0:n} = \{x_0, x_1, \ldots, x_n\}\) 是一个由离散词元序列组成的输入，\(y \in Y\) 是一个标签。我们的目标是估计分类的条件概率 \(f_M(x) = \hat{p}(y\\|x)\)，其中模型 \(M\) 的参数可以进行微调，也可以保持冻结。

设 $[D_i]$ 是一个离散提示词元。每个提示可以用一个模板 $T = {[D_{0:i}], x, [D_{(i + 1):j}], y, [D_{(j + 1):k}]}$ 来描述，该模板可以将标注数据（包括输入 $x$ 和标签 $y$）组织成一个文本词元序列，从而可以将任务重新表述为填充输入文本中的空白。例如，对于预测一个国家首都的任务，一个提示可以是 “[INPUT] 的首都是 [LABEL]”。对于一条标注数据 “(英国, 伦敦)”，重新表述后的文本将是 “英国的首都是 [MASK]”，其中 “[MASK]” 应该预测出给定的标签 “伦敦”。离散提示和离散数据都会通过预训练的嵌入层映射到输入嵌入：

\[\{e(D_0)\ldots e(D_i), e(x_0), \ldots, e(x_n), \ldots, e(D_k)\}\]

其中 $e \in \mathbb{R}^{|V| \times d}$。

这样的离散提示往往极其不稳定，并且在反向传播时可能不是最优的。P-Tuning 使用连续提示嵌入来改进和稳定提示学习。设 $[P_i]$ 是第 $i$ 个连续提示嵌入。P-Tuning 的提示模板如下：

\[T = \{[P_{0:i}], x, [P_{(i + 1):j}], y, [P_{(j + 1):k}]\}\]

P-Tuning 利用一个额外的嵌入函数 $f: [P_i] \to h_i$ 将模板映射为：

\[\{h_0, \ldots, h_i, e(x), h_{i + 1}, \ldots, h_j, e(y), h_{j + 1}, \ldots, h_k\}\]

最后，更新嵌入 ${P_i}_{i = 1}^k$ 以优化任务损失函数。

值得注意的是，也可以将离散提示和连续提示拼接起来，这种方法效果更好。

在上述框架中，采用一个映射函数 $f$ 将可训练嵌入 ${P_i}$ 映射到模型输入 ${h_i}$。其背后的直觉是，与使用独立的可学习嵌入相比，使用映射函数能更方便地对不同提示嵌入之间的依赖关系进行建模。P-Tuning 分别对长短期记忆网络（LSTM）、多层感知机（MLP）以及恒等映射函数进行了实验。

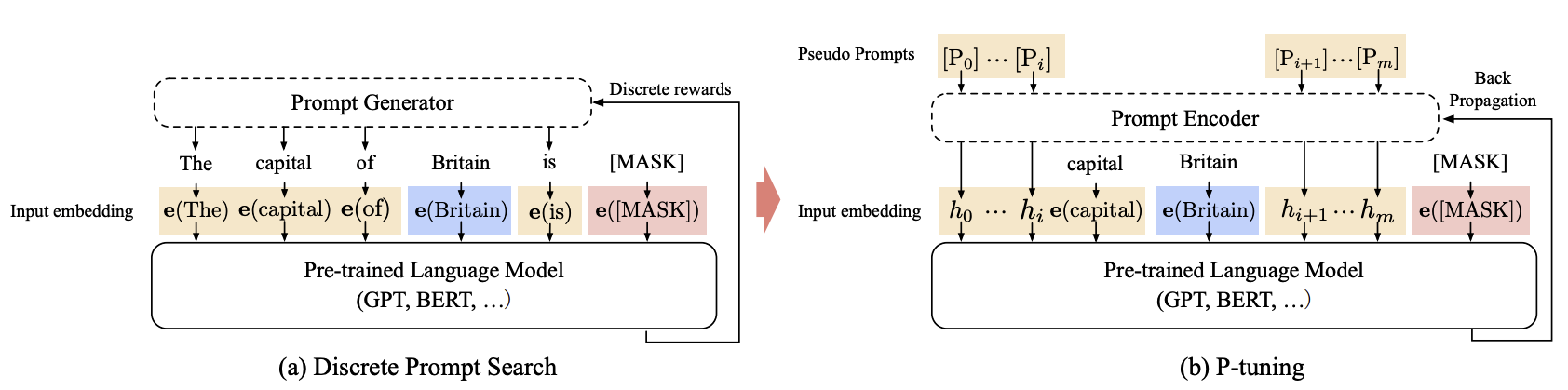
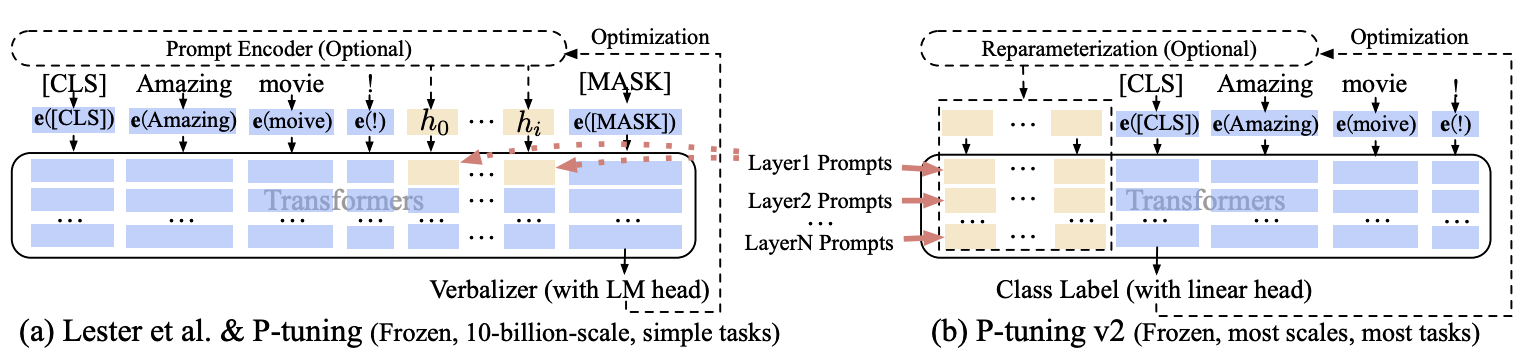
如图，对于 “英国的首都是 [MASK]” 的提示搜索示例。给定上下文（蓝色区域，“英国”）和目标（红色区域，“[MASK]”），橙色区域指的是提示。在（a）中，提示生成器仅接收离散奖励；相反，在（b）中，连续提示嵌入和提示编码器可以以可微的方式进行优化。

P-Tuning V1 只在输入的时候加入 embedding 进行调整，且其位置可以自由选择，而 Prefix Tuning 更新的是每一层中与虚拟 token 位置对应的所有参数，包括 embedding 层以及虚拟 token 位置对应的每一层的 activation。

P-Tuning V2

P-Tuning V1 在当模型规模不大时，特别是小于 100 亿参数时，其表现远不如微调。此外，与微调相比，在一些困难的序列标注任务（如抽取式问答）上的表现不佳。

考虑到这些挑战，P-Tuning v2 采用深度提示调优（deep prompt tuning），作为一种适用于不同规模模型和自然语言理解任务的通用解决方案。

如 P-Tuning V1，连续提示仅被插入到输入嵌入序列中（参见上图（a））。这带来了两个问题。其一，由于序列长度的限制，可调节的参数数量有限。其二，输入嵌入对模型预测的影响相对间接。

为应对这些问题，P-Tuning v2 采用了深度提示调优的理念（如：Prefix Tuning）。如图所示，不同层的提示作为前缀词元被添加。一方面，P-Tuning v2 拥有更多可调节的特定任务参数（从 $0.01\%$ 增加到 $0.1\% - 3\%$），在保证参数高效的同时，为每个任务提供了更大的容量；另一方面，添加到更深层的提示对模型预测的影响更为直接。

为实现最佳性能，优化和实现过程中有一些实用的细节：

1. 重新参数化
   • 先前的工作通常利用诸如多层感知机（MLP）这样的重新参数化编码器来转换可训练的嵌入。然而，对于自然语言理解任务，P-Tuning v2 发现其效果取决于具体的任务和数据集。在一些数据集上 MLP 对结果的影响甚微，甚至产生负面影响
2. 提示长度
   • 提示长度在 P-Tuning v2 中起着关键作用。一般来说，简单的分类任务更适合较短的提示（少于 20）；而复杂的序列标注任务则更倾向于较长的提示（约 100）
3. 多任务学习
   • 多任务学习在针对单个任务进行微调之前，利用共享的连续提示对多个任务进行联合优化
4. 分类头
   • 使用语言模型头来预测表述词（verbalizers）一直是提示调优（prompt tuning）的核心方法，但在全数据设置中这并不是必需的，并且与序列标注任务不兼容。类似于 BERT，P-tuning v2 在 token 上方应用一个随机初始化的分类头

Prompt Tuning

Prompt Tuning 可以看作是 Prefix Tuning 的简化版本，其只在输入层加入可学习的提示词，而非 Prefix Tuning 通过 MLP 来调整前缀部分的参数。

提示（Prompting）是一种在模型生成 $Y$ 的过程中为其提供额外信息以供参考的方法。通常情况下，提示的实现方式是在输入 $X$ 前添加一系列词元 $P$，这样模型在保持参数 $\theta$ 固定的同时，最大化正确输出 $Y$ 的似然 $Pr_{\theta}(Y \mid [P; X])$。

在 GPT-3 中，提示词元 $P = \{p_1, p_2, \ldots, p_n\}$ 的表示是模型嵌入表（embedding table）的一部分，由冻结的参数 $\theta$ 进行参数化。因此，要找到最优提示，就需要通过手动搜索或不可微搜索方法来选择提示词元。

Prompt Tuning 去除了提示 $P$ 必须由 $\theta$ 进行参数化的限制；相反，提示有其独立的参数 $\theta_P$，这些参数可以进行更新。

在提示设计（prompt design）中，涉及从固定的、参数冻结的词汇表中选择提示词元，这些词元的嵌入（embedding）是固定的。而提示调优（prompt tuning）可以看作是使用一个由特殊词元组成的固定提示，其中只有这些提示词元的嵌入可以被更新。

新的条件生成模型现在表示为 $Pr_{\theta; \theta_P}(Y \mid [P; X])$，可以通过反向传播最大化 $Y$ 的似然来进行训练，并且只对 $\theta_P$ 应用梯度更新。

给定一系列 $n$ 个词元 $\{x_1, x_2, \ldots, x_n\}$，T5 首先会对这些词元进行嵌入，形成一个矩阵 $X_e \in \mathbb{R}^{n \times e}$，其中 $e$ 是嵌入空间的维度。Prompt Tuning 的软提示（Soft Prompt）表示为一个参数 $P_e \in \mathbb{R}^{p \times e}$，其中 $p$ 是提示的长度。

然后，将提示与嵌入后的输入进行拼接，形成一个单一的矩阵 $[P_e; X_e] \in \mathbb{R}^{(p + n) \times e}$，该矩阵随后像往常一样通过 编码器-解码器。训练模型以最大化 $Y$ 的概率，但仅更新提示参数 $P_e$。

Soft Prompt 伪代码示例：

3.1.3、其他 Additive 方法

除了上述方法之外，还有其他一些方法会在微调过程中策略性地引入额外的参数。例如，(IA)³ 引入了三个可学习的缩放向量：$l_k \in \mathbb{R}^{d_k}$、$l_v \in \mathbb{R}^{d_v}$ 和 $l_{ff} \in \mathbb{R}^{d_{ff}}$，分别用于对键、值和前馈网络（FFN）的激活值进行缩放，如下图中 (a) 所示。自注意力模块内的操作可以描述如下：

\[SA(x) = Softmax\left(\frac{Q \odot (l_k \odot K^T)}{\sqrt{d_{head}}}\right) \odot (l_v \odot V) \tag{9}\]

在前馈网络中，缩放操作可以表示为：

\[FFN_{Transformer}(x) = W_{up} \odot (l_{ff} \odot \sigma(W_{down}x)) \tag{10}\]

其中 $\odot$ 表示哈达玛积。此外，缩放向量 $l_k$ 和 $l_v$ 可以无缝地整合到 $A_Q$ 和 $A_W$ 的权重矩阵中。这种整合有效地消除了推理过程中的额外计算成本。

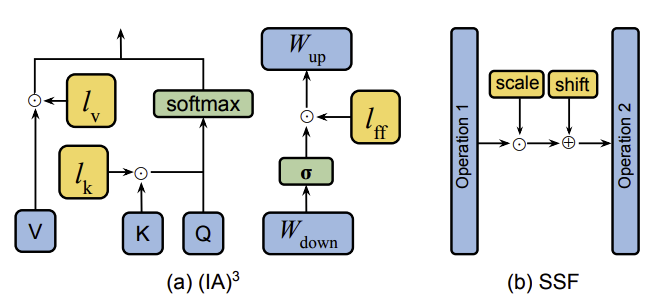
一种类似的技术——可缩放移位融合（SSF，Scalable Shift Fusion）也对模型的激活值进行线性变换，如图中(b) 所示。具体来说，在预训练模型的每个操作（即多头自注意力（MSA）、前馈网络和层归一化）之后，会插入一个 SSF-ADA 层，该层对操作产生的特征进行缩放和平移。在微调过程中，只有这些 SSF-ADA 层可以被更新；而在推理过程中，与 (IA)³ 类似，这些 SSF-ADA 层可以合并到模型权重中，因此不会产生额外的推理开销。

推理时策略适配器（IPA，Inference-Time Policy Adapters）提供了一种新颖的方法，可在不修改基础大语言模型（LLM）参数的情况下，使其符合用户的特定需求。当处理参数极其庞大且通常无法直接访问的模型时，这一点尤为重要。IPA 通过在解码阶段将基础大语言模型的输出分布（基础策略）与一个较小规模模型的输出分布（适配器策略）进行组合（通过乘法和归一化）来实现这一目标。在训练过程中，使用强化学习对策略适配器的参数进行微调，而基础策略的参数保持不变。在推理过程中，IPA 使用基础模型和经过训练的策略适配器的组合分布进行解码，以满足用户定义的特定标准。

3.2、Selective PEFT

与通过增加更多参数来提高模型复杂度的 additive PEFT 不同，Selective PEFT 会对现有参数的一个子集进行微调，以提升模型在下游任务上的性能。

具体而言，给定一个参数为 $\theta = {\theta_1, \theta_2, …, \theta_n}$ 的模型，其中每个 $\theta_i$ 表示一个单独的模型参数，$n$ 表示这些参数的总数。选择性参数高效微调的过程是通过对这些参数应用一个二进制掩码 $M = {m_1, m_2, …, m_n}$ 来表示的。$M$ 中的每个 $m_i$ 取值为 0 或 1，分别表示对应的参数 $\theta_i$ 是否被选中（1 表示选中，0 表示未选中）进行微调。微调后更新的参数集 $\theta’$ 由下式给出：

\[\theta'_i = \theta_i - \eta \cdot m_i \cdot \frac{\partial L}{\partial \theta_i} \tag{11}\]

其中，$\eta$ 表示学习率，$\frac{\partial L}{\partial \theta_i}$ 是损失函数关于参数 $\theta_i$ 的梯度。在这个公式中，只有被选中的参数（即 $m_i = 1$）会在反向传播过程中被更新。

Diff pruning 是一项具有代表性的工作，它在微调过程中对模型权重应用了一个可学习的二进制掩码。为了实现参数高效性，该掩码通过对 $L_0$ 范数惩罚项的可微近似进行正则化。

PaFi 简单地选择绝对值最小的模型参数作为可训练参数。

FishMask 使用近似费舍尔信息来确定参数的重要性，然后根据该信息选择前 $k$ 个参数来构成掩码 $M$。

类似地，Fish-Dip 也使用费舍尔信息来计算 $M$，但该掩码会在每个训练周期中动态重新计算。

LT-SFT 引入了另一种确定参数重要性的技术，其灵感来源于彩票假设（Lottery Ticket Hypothesi），即选择在初始微调阶段变化最大的参数子集来构成掩码 $M$。

SAM 提出了一种二阶近似方法，该方法用一个解析可解的优化函数来近似原始问题，以帮助确定参数掩码。

Child-tuning 提出了两种在每次训练迭代中选择子网络的方法，只有该子网络内的参数可以被更新。

然而，上述非结构化的参数掩码会导致非零掩码分布不均匀，并且在实现参数高效微调时会降低硬件效率。如图所示，结构化掩码以规则的模式组织参数掩码，与随机应用的非结构化掩码不同，因此在训练过程中提高了计算和硬件效率。因此，各种结构化的选择性参数高效微调技术得到了广泛研究。差分剪枝通过将权重参数划分为局部组并策略性地一起消除它们，提出了一种结构化剪枝策略。

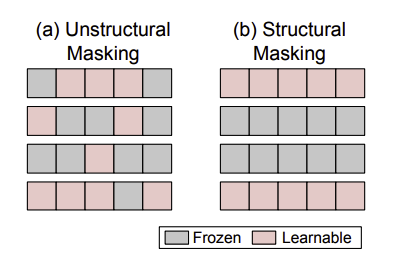
类似地，FAR 通过将 Transformer 模块中前馈网络（FFN）的权重分组为节点，然后使用 $L_1$ 范数对这些学习节点进行排序和选择，来微调 BERT 模型。为了进一步降低内存访问频率，他们还通过对学习节点进行分组来重新配置前馈网络。

Bitfit 被提出用于仅微调每个深度神经网络（DNN）层的偏置参数，并在小模型上取得了有竞争力的结果。然而，这种方法无法处理大模型。S-BitFit 将 NAS 应用于 Bitfit，其中 S-BitFit 保留了偏置参数调优的结构化特性，即限制神经架构搜索算法必须为每个偏置模块选择 $\delta b$ 是否为 0。

与在 Transformer 中微调特定模块的偏置参数调优类似，Xattn Tuning 仅微调交叉注意力层。

敏感感知的视觉参数高效微调（SPT）首先确定通过调优时损失减少来衡量的敏感参数。这种敏感性是使用一阶泰勒展开计算的，该展开是在微调前通过一次前向和反向传播一次性得出的。接下来，SPT 找出敏感参数数量超过预定义阈值的权重矩阵，然后对这些目标权重应用选定的参数高效微调技术（例如，低秩自适应（LoRA）和适配器）以实现结构化调优。

3.3、Reparameterized PEFT

重参数化（Reparameterized）指的是通过变换模型的参数，将模型架构从一种形式等效转换为另一种形式。在 PEFT 的背景下，这通常意味着构建低秩参数化，以在训练过程中实现参数高效的目标。在推理时，模型可以转换回其原始的权重参数化形式，从而确保推理速度不变。

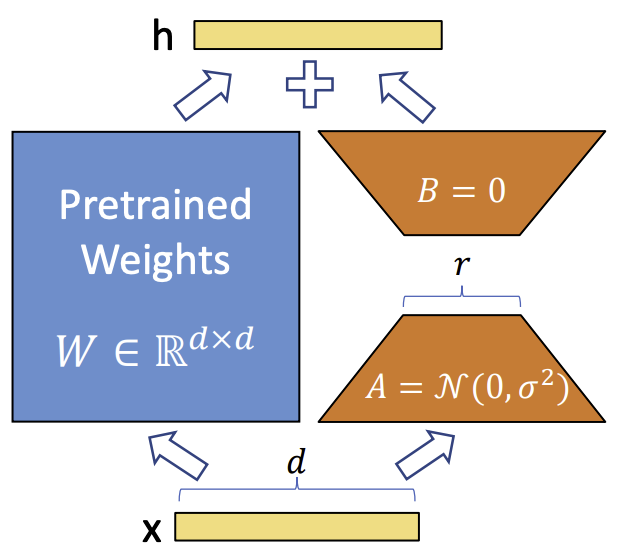
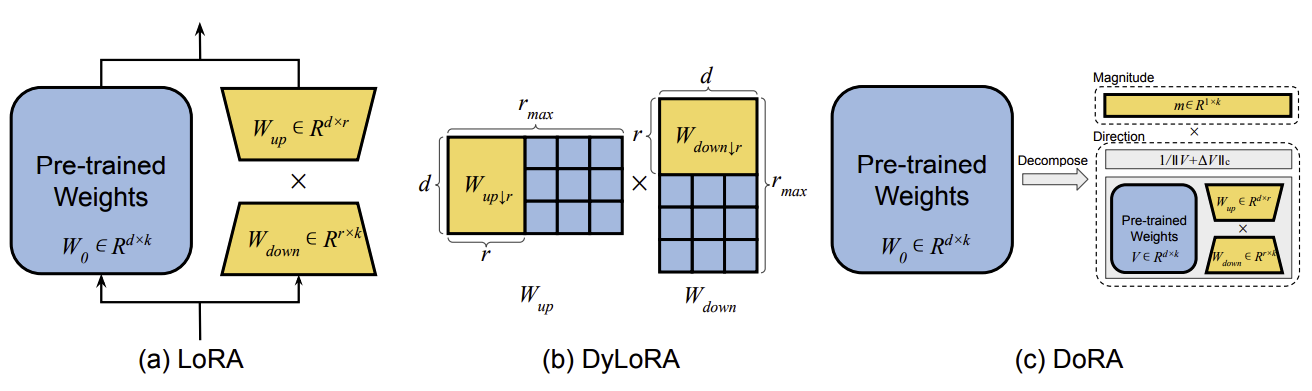
早期的研究表明，常见的预训练模型呈现出极低的内在维度。换句话说，有可能找到一种低维的重参数化形式，其在微调时的效果与整个参数空间相当。Intrinsic SAID 是研究 LLM 微调过程中内在维度特征的开创性工作。然而，最广为人知的重参数化技术是低秩自适应（LoRA），如下图中（a）所示。对于给定的预训练权重矩阵 $W_0 \in \mathbb{R}^{d\times k}$，LoRA 引入了两个可训练的权重矩阵 $W_{up} \in \mathbb{R}^{d\times r}$ 和 $W_{down} \in \mathbb{R}^{r\times k}$，其中秩 $r \ll \min(d, k)$，它们与 $W_0$ 并行操作。

设 $h_{in}$ 表示输入。在正常情况下，通过 $W_0$ 的输出为 $h_{out} = W_0h_{in}$。而 LoRA 通过引入一个包含特定任务知识的增量更新 $\Delta W$ 来修改这个输出：

\[h_{out} = W_0h_{in} + \frac{\alpha}{r} \Delta W h_{in} = W_0h_{in} + \frac{\alpha}{r} W_{up}W_{down}h_{in} \tag{12}\]

其中 $\alpha$ 表示缩放因子。在训练开始时，$W_{down}$ 使用随机高斯分布进行初始化，而 $W_{up}$ 初始化为零，以确保 $\Delta W$ 最初的值为零。

LoRA 易于实现，并且已经在参数多达 1.75 万亿的模型上进行了评估。一旦微调完成，LoRA 的自适应权重会无缝集成到预训练的骨干权重中。这种集成确保了 LoRA 在推理过程中不会增加额外负担，从而保持了模型的效率。

在 LoRA 训练中，选择合适的秩一直是一个具有挑战性的问题。为了解决这个问题，DyLoRA，如图中（b）所示，在预定义的训练预算内，在一系列秩上训练 LoRA 模块，而不是使用单一的固定秩。具体来说，对于给定的秩范围 $R = \{r_{min}, r_{min}+1, \ldots, r_{max}\}$，DyLoRA 在训练过程的每次迭代中动态选择一个秩 $r \in R$。因此，矩阵 $W_{down}$ 和 $W_{up}$ 会针对所选的秩 $r$ 进行调整，得到截断版本 $W_{down}\downarrow r = W_{down}[1 : r, :]$ 和 $W_{up}\downarrow r = W_{up}[:, 1 : r]$，并且在这次迭代中的后续前向和反向传播将仅在 $W_{down}\downarrow r$ 和 $W_{up}\downarrow r$ 上进行，而不是在 $W_{down}$ 和 $W_{up}$ 上进行。通过这种动态且无需搜索的方法，DyLoRA 显著减少了为特定任务找到最优且固定的 LoRA 秩所需的训练时间。

AdaLoRA 使用奇异值分解（SVD）对 $\Delta W$ 进行重新表述，记为 $\Delta W = P \Lambda Q$，其中 $P \in \mathbb{R}^{d\times r}$ 和 $Q \in \mathbb{R}^{r\times k}$ 是正交矩阵，$\Lambda$ 是包含奇异值 ${\lambda_i}_{1\leq i\leq r}$ 的对角矩阵。所有三个权重矩阵都设置为可学习的。在训练过程中，根据奇异值的重要性得分迭代地对其进行剪枝，这些重要性得分由 梯度-权重 乘积的移动平均值构建而成。为了确保 $P$ 和 $Q$ 之间的正交性，即 $P^T P = QQ^T = I$，在损失函数中加入了一个额外的正则化项：

\[R(P, Q) = \|P^T P - I\|_F^2 + \|QQ^T - I\|_F^2 \tag{13}\]

这种自适应方法使模型能够在每个 LoRA 模块内动态调整秩，根据权重矩阵的重要性有效管理其参数数量。

然而，根据结构化低秩自适应（SoRA）的研究，AdaLoRA 中使用的重要性得分是启发式构建的，缺乏严格的理论依据。此外，移动平均操作和等式（13）的计算在训练过程中会引入额外的计算成本。为了解决这个问题，SoRA 消除了 $P$ 和 $Q$ 的正交性前提。相反，直接在 $W_{up}$ 和 $W_{down}$ 之间应用并优化一个门控单元 $g \in \mathbb{R}^r$：

\[h_{out} = W_{up}(g \odot (W_{down}h_{in})) \tag{14}\]

其中 $\odot$ 表示哈达玛积。门控单元 $g$ 使用针对 $l_1$ 损失的近端梯度迭代的一种变体进行更新，这种方法具有明确的数学意义，不需要启发式前提。训练完成后，通过移除 $W_{down}$ 和 $W_{up}$ 中对应的列和行来剪枝归零的门控单元。

随后的几项研究旨在从各个方面改进 LoRA 的性能。例如，Laplace-LoRA 注意到微调后的大语言模型通常表现出过度自信的问题。为了提高微调后大语言模型的校准度，Laplace-LoRA 采用贝叶斯方法，具体来说是对 LoRA 参数的后验分布进行事后拉普拉斯近似。

LoRA Dropout 向可学习的低秩矩阵引入随机噪声，并增加参数稀疏性，以降低过拟合的风险。

LoRA+ 提出为 LoRA 矩阵 $W_{down}$ 和 $W_{up}$ 设置不同的学习率，即 $\eta_{up} = \lambda\eta_{down}$，其中 $\lambda > 1$ 为固定值，并调整 $\eta_{down}$。

MoSLoRA（Mixture-of-Subspaces LoRA）通过结构重参数化将 LoRA 分解为子空间，然后使用一个可学习的混合器（与原始 LoRA 权重一起训练）来融合这些子空间。与 LoRA 类似，MoSLoRA 也可以合并到原始权重中。

得益于 LoRA 的模块化设计，许多研究在其框架中纳入了多个 LoRA 模块以提高性能。例如，LoRAHub 聚合了在不同任务上训练的各种 LoRA 模块。给定来自新任务的少量示例，LoRAHub 可以通过无梯度方法 Shiwa 自动组合兼容的 LoRA 模块，无需人工干预。

MOELoRA 采用专家混合（MOE）方法在多任务设置下训练 LoRA，从而得到多个专家 LoRA 模块。为了为特定任务检索参数，MOELoRA 使用一个基于任务的门控函数，该函数根据任务 ID 为每个专家分配贡献权重，最终参数通过所有专家的加权和计算得出。

除了 LoRA 之外，还有其他几种重参数化技术正在兴起，具有巨大的潜力。例如，Compacter 通过将 $W_{down}$ 和 $W_{up}$ 参数化为 $W = \sum_{i = 1}^{n} A_i \otimes B_i$，引入了轻量级适配器模块，其中 $A_i \in \mathbb{R}^{n\times n}$，$B_i \in \mathbb{R}^{\frac{r}{n} \times \frac{d}{n}}$，$\otimes$ 表示克罗内克积。他们通过将 $A_i$ 指定为共享参数，并使用两个低秩矩阵的乘积对 $B_i$ 进行重参数化，进一步减少了参数数量，有效地将参数复杂度从 $O(rd)$ 降低到 $O(r + d)$。

相关研究，如 KronA 和 KAdaptation，也使用克罗内克积对适配器权重进行重参数化，旨在实现参数减少。

HiWi 提出了一种适配器微调方法，该方法直接将适配器应用于预训练参数，而不是隐藏表示，具体如下：

\[W' = W + \sigma(W W_{down})W_{up} \tag{15}\]

其中 $W$ 表示 Transformer 模块前馈层内的权重或偏置。值得注意的是，在推理时，该方法会预先计算 $W’$，确保模型的推理延迟与传统的全量微调相当。基于 Vector-based Random Matrix Adaptation（VeRA）采用一对在所有层共享的冻结低秩矩阵 $W_{up}$ 和 $W_{down}$，并通过学习表示为 $b$ 和 $d$ 的小的可训练缩放向量（正式表示为对角矩阵 $\Lambda_b$ 和 $\Lambda_d$）来调整这些矩阵。具体来说，重参数化形式如下：

\[h_{out} = W_0h_{in} + \Lambda_bW_{up}\Lambda_dW_{down}h_{in} \tag{16}\]

其中 $W_{up}$ 和 $W_{down}$ 均使用随机高斯分布进行初始化。与 LoRA 类似，缩放向量 $b$ 初始化为零，以确保在第一次前向传播时权重矩阵不受影响。与 LoRA 相比，这种方法显著减少了可训练参数的数量，同时保持了相同的性能，使得在单个 GPU 上对更大的模型进行微调成为可能。

Weight-Decomposed Low-Rank Adaptation（DoRA）提出了一种新颖的方法，将模型权重 $W_0 \in \mathbb{R}^{d\times k}$ 分解为大小和方向，如下所示：

\[W_0 = m \frac{V}{\|V\|_c} = \|W_0\|_c \frac{W_0}{\|W_0\|_c} \tag{17}\]

其中 $m \in \mathbb{R}^{1\times k}$ 是大小向量，$V \in \mathbb{R}^{d\times k}$ 是方向矩阵，$|\cdot|_c$ 是矩阵每列的向量范数。随后，DoRA 对 $m$ 和 $V$ 采用独特的微调策略。虽然两者都是可调整的，但只有 $V$ 进行 LoRA 重参数化，定义如下：

\[W' = m \frac{V + \Delta V}{\|V + \Delta V\|_c} = m \frac{W_0 + W_{up}W_{down}}{\|W_0 + W_{up}W_{down}\|_c} \tag{18}\]

其中 $\Delta V$ 是通过 LoRA 学习到的增量方向更新，下划线参数表示可训练参数。通过这种方法，DoRA 在各种任务和模型上始终优于 LoRA，证明了其优越性。

LoRA

低秩自适应（Low-Rank Adaptation，LoRA）冻结预训练模型的权重，并将可训练的低秩分解矩阵注入到 Transformer 架构的每一层中，从而大幅减少下游任务的可训练参数数量。

早期有研究表明，学习得到的过度参数化模型实际上处于一个低内在维度空间。LoRA 假设，在模型自适应过程中权重的变化也具有较低的 “内在秩”，由此提出了低秩自适应（Low-Rank Adaptation，LoRA）方法。

如下图所示，LoRA 允许在保持预训练权重冻结的情况下，通过优化神经网络中某些全连接层在自适应过程中权重变化的低秩分解矩阵，来间接训练这些全连接层。以 1750 亿参数的 GPT-3 模型为例，即使全秩（即图中的 $d$）高达 12288，极低的秩（即图中的 $r$ 可以为 1 或 2）就已足够，这使得 LoRA 在存储和计算方面都非常高效。

LoRA 具有以下几个关键优势：

• 模型复用与任务切换高效：一个预训练模型可以被共享，并用于为不同任务构建多个小型的 LoRA 模块。可以冻结共享模型，通过替换上图中的矩阵 A 和 B 来高效地切换任务，从而显著降低存储需求和任务切换开销
• 训练高效且降低硬件门槛：当使用自适应优化器时，由于无需为大多数参数计算梯度或维护优化器状态，只需优化注入的、规模小得多的低秩矩阵，因此 LoRA 使训练更加高效，并将硬件入门门槛降低至原来的三分之一
• 无额外推理延迟：简单的线性设计允许在部署时将可训练矩阵与冻结的权重合并，从设计上保证了与全量微调模型相比，不会引入额外的推理延迟
• 可与其他方法结合：LoRA 与许多现有方法是正交的，可以与它们结合使用，例如前缀调优（prefix-tuning）

0、前置知识

矩阵的秩是指矩阵中线性无关的行向量或者列向量的最大数目。可以分为行秩和列秩，并且对于任何一个矩阵，其行秩等于列秩。例如，对于一个 $m \times n$ 的矩阵 $A$，它的秩记为 $rank(A)$ 或者 $r(A)$，并且满足 $0 \leq rank(A) \leq \min(m, n)$。

在 LoRA 中，研究者假设在模型自适应过程中权重矩阵的更新 $\Delta W$ 具有较低的 “内在秩”。因此可以将更新 $\Delta W$ 表示为两个低秩矩阵的乘积 $\Delta W = BA$，其中 $B \in \mathbb{R}^{d\times r}$，$A \in \mathbb{R}^{r\times k}$，并且 $r \ll \min(d, k)$ 。这里的 $r$ 就是低秩矩阵的秩，通过将更新矩阵约束为低秩形式，可以用较少的参数（即矩阵 $B$ 和 $A$ 中的参数）来表示权重的更新，从而减少可训练参数的数量，降低计算和存储成本，同时在一定程度上保持模型的性能。

1、问题陈述

将 Transformer 层的输入和输出维度大小称为 $d_{model}$，用 $W_q$、$W_k$、$W_v$ 和 $W_o$ 分别表示自注意力模块中的 query/key/value/output 投影矩阵。$W$ 或 $W_0$ 表示预训练权重矩阵，$\Delta W$ 表示其在自适应过程中累积的梯度更新。

用 $r$ 表示 LoRA 模块的秩。使用 Adam 优化器进行模型优化，并使用 Transformer 多层感知机（MLP）前馈层，其维度 $d_{ffn} = 4 \times d_{model}$。

假设有一个由参数 $\varPhi$ 进行参数化的预训练自回归语言模型 $P_{\varPhi}(y \mid x)$。例如，$P_{\varPhi}(y \mid x)$ 可以是一个通用的多任务学习模型，如基于 Transformer 架构的 GPT。考虑将这个预训练模型适配到下游的条件文本生成任务，每个下游任务由一个 context-target pairs 的训练数据集表示：$\mathcal{Z} = \{(x_i, y_i)\}_{i = 1,\ldots,N}$，其中 $x_i$ 和 $y_i$ 都是词元序列。

在全量微调过程中，模型初始化为预训练权重 $\varPhi_0$，并通过反复沿着梯度方向更新到 $\varPhi_0 + \Delta\varPhi$，以最大化条件语言建模目标：

\[\max_{\varPhi}\sum_{(x,y)\in Z}\sum_{t = 1}^{|y|}\log (P_{\varPhi}(y_t|x, y_{<t})) \quad (1)\]

全量微调的一个主要缺点是，对于每个下游任务，都会学习一组不同的参数 $\Delta\varPhi$，其维度 $|\Delta\varPhi|$ 等于 $|\varPhi_0|$。因此，如果预训练模型规模很大（例如 GPT-3，即 $|\varPhi_0| \approx 1750$ 亿），那么存储和部署多个独立的微调模型实例即便可行，也会极具挑战性。

LoRA 采用一种更节省参数的方法，其中特定任务的参数增量 $\Delta\varPhi = \Delta\varPhi(\varTheta)$ 由一组规模小得多的参数 $\varTheta$ 进一步编码，且 $|\varTheta| \ll |\varPhi_0|$。因此，寻找 $\Delta\varPhi$ 的任务就变成了对 $\varTheta$ 进行优化：

\[\max_{\varTheta}\sum_{(x,y)\in \mathcal{Z}}\sum_{t = 1}^{|y|}\log (p_{\varPhi_0+\Delta\varPhi(\varTheta)}(y_t|x, y_{<t})) \quad (2)\]

使用一种低秩表示来编码 $\Delta\varPhi$，这种表示在计算和内存使用方面都很高效。当预训练模型是 1750 亿参数的 GPT-3 时，可训练参数的数量 $|\varTheta|$ 可以小至 $|\varPhi_0|$ 的 $0.01\%$。

2、现有的解决方案不够好吗？

以语言建模为例，在高效自适应方面有两种显著的策略：添加适配器层（如：Serial Adapter Tuning）或者优化输入层激活的某些形式（如：Prefix Tuning、Prompt Tuning、P-Tuning）。然而，这两种策略都有其局限性。

适配器层会引入推理延迟，该设计在每个 Transformer 块中添加适配器层，虽然可以通过裁剪层或利用多任务设置来减少总体延迟，但没有直接的方法可以绕过适配器层中的额外计算。虽然适配器参数较少，然而，大型神经网络依靠硬件并行性来降低延迟，而适配器层必须按顺序处理。这在在线推理场景中会产生影响，因为在线推理的批量大小通常小至 1。

直接优化提示（Prompt）很困难，如 Prefix Tuning 很难进行优化，并且其性能在可训练参数方面呈现非单调变化。更根本的是，为自适应预留一部分序列长度必然会减少可用于处理下游任务的序列长度，这使得提示调优的性能可能不如其他方法。

3、低秩参数化更新矩阵

神经网络包含许多执行矩阵乘法的全连接层。这些层中的权重矩阵通常是满秩的。在适配特定任务时，预训练语言模型具有较低的 “内在维度”，并且即使随机投影到一个较小的子空间，仍然可以有效地学习。受此启发，假设在适配过程中，权重的更新也具有较低的 “内在秩”。

对于一个预训练的权重矩阵 $W_0 \in \mathbb{R}^{d\times k}$，通过低秩分解来约束其更新，即 $W_0 + \Delta W = W_0 + BA$，其中 $B \in \mathbb{R}^{d\times r}$，$A \in \mathbb{R}^{r\times k}$，且秩 $r \ll \min(d, k)$。

在训练期间，$W_0$ 被冻结，不会接收梯度更新，而 $A$ 和 $B$ 包含可训练参数。注意，$W_0$ 和 $\Delta W = BA$ 都与相同的输入相乘，并且它们各自的输出向量按元素相加。对于 $h = W_0x$，LoRA 修改后的前向传播过程得到：

\[h = W_0x + \Delta W x = W_0x + BAx\]

对 $A$ 使用随机高斯初始化，对 $B$ 使用零初始化，因此在训练开始时 $\Delta W = BA$ 为零。然后，将 $\Delta W x$ 乘以 $\frac{\alpha}{r}$，其中 $\alpha$ 是 $r$ 中的一个常数。当使用 Adam 优化器进行优化时，如果适当地缩放初始化，调整 $\alpha$ 大致等同于调整学习率。因此，简单地将 $\alpha$ 设置为我们尝试的第一个 $r$ 值，并且不再对其进行调整。这种缩放有助于减少在改变 $r$ 时重新调整超参数的需求。

3.1、全微调的泛化

更通用的微调形式允许对预训练参数的一个子集进行训练。LoRA 更进一步，不要求在适配过程中权重矩阵的累积梯度更新具有满秩。这意味着，当对所有权重矩阵应用 LoRA 并训练所有偏置时，通过将 LoRA 的秩 $r$ 设置为预训练权重矩阵的秩，我们大致可以恢复全量微调的表达能力。换句话说，随着可训练参数数量的增加，训练 LoRA 大致会收敛到训练原始模型，而基于适配器的方法会收敛到一个多层感知机，基于前缀的方法会收敛到一个无法处理长输入序列的模型。

3.2、无额外推理延迟

在生产部署时，可以显式地计算并存储 $W = W_0 + BA$，并像往常一样进行推理。注意，$W_0$ 和 $BA$ 都属于 $\mathbb{R}^{d\times k}$。当需要切换到另一个下游任务时，可以通过减去 $BA$ 恢复 $W_0$，然后加上不同的 $B’A’$，这是一个快速操作，内存开销非常小。关键的是，从设计上保证了与微调模型相比，LoRA 在推理过程中不会引入任何额外的延迟。

4、将 LoRA 应用于 Transformer

在 Transformer 架构中，自注意力模块有四个权重矩阵（$W_q$、$W_k$、$W_v$、$W_o$），MLP 模块有两个权重矩阵。将 $W_q$（或 $W_k$、$W_v$）视为一个维度为 $d_{model} \times d_{model}$ 的单一矩阵，即使输出维度通常会被划分为多个注意力头。

LoRA 最显著的好处是减少了内存和存储的使用。对于使用 Adam 优化器训练的大型 Transformer，如果 $r \ll d_{model}$，由于不需要为冻结的参数存储优化器状态，LoRA 最多可以将显存（VRAM）使用量减少 2/3。在 1750 亿参数的 GPT-3 模型上，LoRA 将训练期间的显存消耗从 1.2 TB 减少到 350 GB。当 $r = 4$ 且仅适配查询和值投影矩阵时，检查点大小大约减少了 10000 倍（从 350 GB 减少到 35 MB）。

这使得能够使用显著更少的 GPU 进行训练，并避免 I/O 瓶颈。另一个好处是，在部署时，可以通过仅交换 LoRA 权重而不是所有参数，以更低的成本在不同任务之间进行切换。这使得在将预训练权重存储在显存中的机器上，可以动态地创建和切换许多定制模型。与全量微调相比，在 1750 亿参数的 GPT-3 模型上训练速度提高了 25%，因为 LoRA 不需要为绝大多数参数计算梯度。

LoRA 也有其局限性。例如，如果为了消除额外的推理延迟而选择将 $A$ 和 $B$ 合并到 $W$ 中，那么在一次前向传播中对具有不同 $A$ 和 $B$ 的不同任务的输入进行批量处理并不直接。不过，在延迟不是关键因素的场景中，可以不合并权重，并为批次中的样本动态选择要使用的 LoRA 模块。

3.4、Hybrid PEFT

不同的 PEFT 方法在不同任务中的效果可能存在显著差异。因此，许多研究旨在结合不同 PEFT 方法的优势，或者通过分析这些方法之间的相似性来建立统一的视角。

例如，UniPELT 将低秩自适应（LoRA）、前缀调优（prefix-tuning）和适配器（adapters）集成到每个 Transformer 模块中。为了控制应该激活哪些 PEFT 子模块，他们还引入了一种门控机制。该机制由三个小型前馈网络（FFN）组成，每个 FFN 产生一个标量值 $G \in (0, 1)$，然后分别应用于 LoRA、前缀和适配器矩阵。在各种设置下，UniPELT 的准确率始终提高了 1% 到 4%。

S4 对几种 PEFT 方法（即适配器（A）、前缀调优（P）、BitFit（B）和 LoRA（L））的设计空间进行了探索，以揭示潜在的设计模式。经过一系列实验发现：

1. 对Transformer层应用纺锤分组分区，形成四个层组 $G_i$，其中$i \in {1 … 4}$。同一组中的层具有相似的行为，这意味着应该应用相似的PEFT策略
2. 将可训练参数的数量均匀分配到各层
3. 对所有组进行调优
4. 在不同组中分配不同的PEFT策略

性能最佳的设计空间如下：

\[G_1 : (A, L)，G_2 : (A, P)，G_3 : (A, P, B)，G_4 : (P, B, L)\]

MAM Adapter 探索了三种附加式 PEFT 方法（适配器、前缀调优和 LoRA）之间的内在相似性，并由此开发出三种变体：并行适配器，将适配器层放置在特定层（自注意力层（SA）或前馈网络层（FFN））旁边，而不是之后；多头并行适配器，将并行适配器划分为多个头，每个头影响自注意力层中的头注意力输出；缩放并行适配器，在并行适配器层之后添加一个缩放项，类似于 LoRA。大量实验表明，最有效的配置是在自注意力层使用前缀调优，在前馈网络层使用缩放并行适配器，这就是所谓的 MAM 适配器。

LLM-Adapters 构建了一个易于使用的框架，将各种 PEFT 技术集成到大语言模型中。通过在多个数据集上进行全面的基准测试，该研究揭示了几个关键见解：

1. 串行适配器、并行适配器和 LoRA 的最有效位置分别是在多层感知机（MLP）层之后、MLP 层旁边以及同时在注意力层和 MLP 层之后
2. 使用 PEFT 的较小大语言模型在某些任务上与较大的模型相比，可以取得有竞争力甚至更优的结果
3. 有了适当的分布内微调数据，较小的模型在特定任务性能上能够超越较大的模型。

一些研究利用 NAS 来寻找更好的 PEFT 组合方法。例如，NOAH 发现不同的 PEFT 配置是专门为不同任务量身定制的。为了解决这个问题，NOAH 采用 NAS 为每个数据集确定最有效的PEFT配置。具体来说，NOAH 的搜索空间包括三种 PEFT 方法：适配器、LoRA 和视觉提示调优（VPT）。它使用一次性神经架构搜索算法 AutoFormer 来高效地发现最优提示模块。

与此类似，AUTOPEFT 首先建立了一个包括串行适配器、并行适配器和前缀调优的搜索空间。然后，他们基于高维多维贝叶斯优化（high-dimensional multi-dimensional Bayesian optimisation）提出了一种有效的 NAS 方法。NOAH 和 AUTOPEFT 都证明了 NAS 在各种任务中改进 PEFT 配置的能力。

4、结论与未来方向

在当前以大模型和大数据集为主导的时代，参数高效微调（PEFT）作为一种能让模型高效适配下游任务的方法，极具吸引力。该技术之所以备受关注，是因为它解决了传统全模型微调带来的重大挑战，传统微调通常对计算资源和数据量有很高的要求。

4.1、简化超参数调优

PEFT 的效果往往对其超参数很敏感，比如适配器的瓶颈维度、LoRA 的秩以及各种 additive PEFT 层的排列方式等。手动调整这些超参数会耗费大量精力。因此，未来的研究可以着重开发那些较少依赖手动调整这些参数的方法，或者自动找到最优的配置设置。

4.2、建立统一的基准测试

尽管已经有像 HuggingFace 的 PEFT 和 AdapterHub 这样的库，但仍然缺乏一个全面的 PEFT 基准测试。这一缺失阻碍了对不同 PEFT 方法的性能和效率进行公平比较。

4.3、提高训练效率

PEFT 假定的参数高效性在训练过程中并不总是能体现在计算和内存节省上。由于可训练参数与预训练模型的架构相互交织，在微调时通常需要对全模型的激活值和梯度进行计算和存储。这种情况需要我们重新思考效率的定义。潜在的解决方案包括结合模型压缩技术（如剪枝和量化），以及专门为优化 PEFT 微调过程中的内存使用而进行的创新。有必要进一步研究提高 PEFT 方法的计算效率。

4.4、探索缩放定律

最初为较小的 Transformer 模型开发的 PEFT 方法，其设计和效果不一定能随着模型规模的增大而扩展。随着基础模型规模的不断增加，识别并调整有效的 PEFT 策略至关重要。这一研究将有助于使 PEFT 方法适应不断发展的大模型架构。

4.5、适配更多模型和任务

各个领域中大型基础模型的兴起为 PEFT 带来了新的机遇。设计出针对像 Sora、Mamba 和 LVM 等模型独特特性的 PEFT 方法，能开拓新的应用场景和机会。

4.6、增强数据隐私

对于系统开发者来说，将个性化的 PEFT 模块交由集中式系统服务或微调还存在信任问题。已经有多种类型的反演攻击被提出，这些攻击通过劫持中间结果来重构用户数据。未来值得信赖的大语言模型系统设计的一个方向是为个人数据以及训练和推理的中间结果开发加密协议。

4.7、结合模型压缩的 PEFT

模型压缩是使大语言模型能够在资源受限的设备上运行的最有效方法之一。然而，模型压缩技术对在硬件上运行的 PEFT 算法性能的影响仍是另一个系统性挑战。像量化和剪枝这样常见的压缩技术需要专门的硬件平台来加速这一过程，为压缩模型构建这样的硬件平台也是未来研究的一个方向。

参考文献

1. Parameter-Efficient Fine-Tuning for Large Models:A Comprehensive Survey
2. Parameter-Efficient Fine-Tuning Methods for Pretrained Language Models: A Critical Review and Assessment
3. Parameter-Efficient Transfer Learning for NLP
4. Prefix-Tuning: Optimizing Continuous Prompts for Generation
5. GPT Understands, Too
6. P-Tuning: Prompt Tuning Can Be Comparable to Fine-tuning Across Scales and Tasks
7. The Power of Scale for Parameter-Efficient Prompt Tuning
8. LORA: LOW-RANK ADAPTATION OF LARGE LANGUAGE MODELS
9. Understanding Parameter-Efficient LLM Finetuning: Prompt Tuning And Prefix Tuning

---

• Previous
  LLM：RAG
• Next
  LLM：Agent

---