1、精排

精排的核心目标是从粗排阶段筛选出的候选集内（通常是几百个到几千个候选文档），依据更加细致的相关性、用户行为、时效性等因素，对文档进行细粒度的排序，以确保最相关的文档排在前面，最大化用户满意度和点击转化率。

精排模型在设计上应该使用更多的特征、更复杂的模型，并且在排序上更加注重细节和上下文的匹配。精排策略的设计上应该重点关注：

特征交叉与深度特征学习
用户序列特征的应用
多目标优化与业务指标的平衡
精排与粗排的协同优化

2、特征

特征设计对于模型的效果至关重要。根据特征来源、结构和时效性的不同，特征可以从多个维度进行划分并设计。

从特征来源上看，可以分为Query特征、User特征、Doc特征、Author特征、交叉特征、级联模型特征、各场景域迁移特征等：

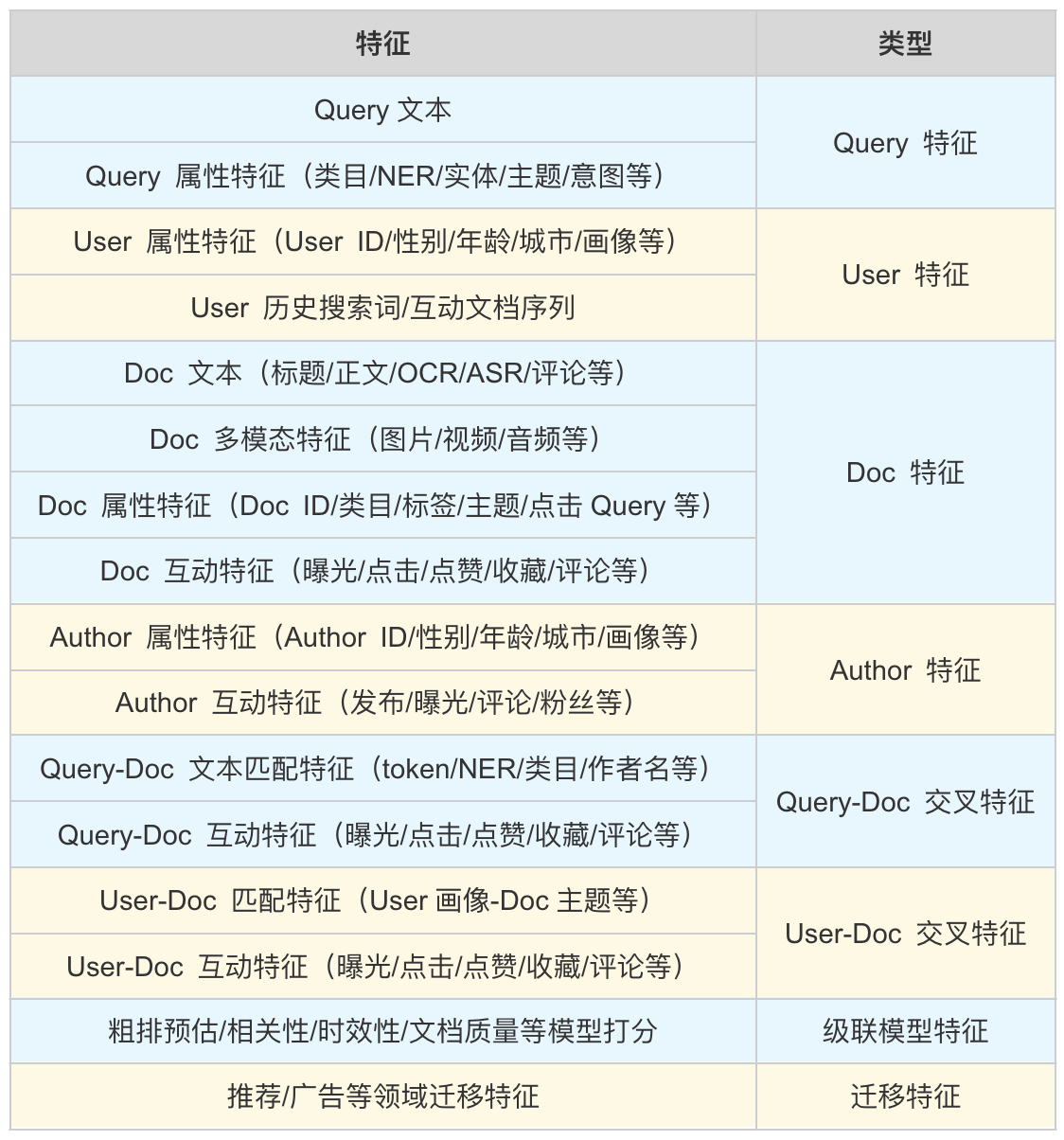
从特征结构上可以划分为：

Dense特征（连续特征）：密集型特征，通常是数值型的，直接输入到神经网络模型中
- 例如：向量特征
Sparse特征（稀疏特征）：稀疏特征一般是离散值，通常通过独热编码（One-hot Encoding）等方法转化为稀疏向量
- 例如：Query、Doc、User等基础离散型类别特征

从特征时效性可以划分为：

离线特征：离线特征是在训练阶段固定生成的特征，通常是基于历史数据或静态信息
- 例如：用户的长期历史行为、文档的基本属性
实时特征：实时特征是在实时搜索或推荐过程中动态生成的特征，通常需要实时获取用户行为或查询的最新信息。
- 例如：用户最近的搜索行为、点击行为、位置、设备类型等

3、训练样本

以点击率（CTR）预估任务为例，精排模型的训练样本中，正样本为曝光后被点击的样本，负样本为曝光后未被点击的样本。

正样本：用户在曝光后点击的记录
负样本：用户在曝光后未点击的记录

除了点击率预估，还应考虑其他行为信号，如点赞、收藏、分享、评论、购买等交互行为。

3.1、样本均衡

由于点击行为稀疏，导致正负样本比例严重失衡，影响模型对正样本的预测准确性。为了降低样本不均衡带来的影响，对于负样本采样通常有以下策略：

均衡高频中长尾样本
- 在曝光未点击的负样本中，按 曝光频率 分层随机抽取负样本，以保证样本均衡频率分布
剔除低置信度样本
- 通过现有模型打分、先验信息、人工/LLM标注等过滤低置信度样本，挖掘难负样本
Skip-Above采样
- 丢弃用户最后一个点击位置以下的样本，避免噪音偏差

此外，样本应该涵盖不同类型和不同标签的 Query 和用户，以便模型学习到多样化的排序规则，避免在中长尾 Query 上预估不准确。

3.2、预估值校准

在采样过程中，由于负样本数量被显著减少，导致采样后的数据分布与实际数据分布不一致，从而引入偏差。因此，模型训练得到的预估点击率 $ \text{pCTR} $ 通常需要通过一定的校正公式来接近真实后验点击率 $ \text{CTR} $。校正公式如下：

\[\text{CTR} = \frac{\text{pCTR} \cdot \text{p}}{\text{pCTR} \cdot \text{p} + (1 - \text{pCTR}) \cdot \text{n}}\]

其中：

$ \text{pCTR} $: 采样后训练的模型输出的预估点击率
$ \text{CTR} $: 真实的点击率
$ \text{p} $: 正样本的采样率
$ \text{n} $: 负样本的采样率

4、模型

精排模型的技术演变经历了从简单的线性模型到复杂的深度学习模型的过程，最早模型采用 Logistic Regression（LR） 线性函数对特征进行建模，由于 LR 无法捕捉高阶特征间的关系，随后加入二阶特征交叉的 Factorization Machines（FM） 模型被提出。在后来的模型演变中，特征交叉的深度和复杂度不断提升。

例如，通过深度神经网络进一步挖掘高阶特征组合的潜力，一些模型引入了多层感知机（MLP）结构，能够对海量特征进行深度融合与抽象，学习到更为复杂和抽象的特征表示，从而显著提升模型对数据中隐藏模式的捕捉能力。同时，注意力机制也被逐渐融入，使得模型能够有针对性地聚焦于关键特征，忽略无关信息，进一步优化特征交叉的效果与效率。

这其中，实现低阶显式交叉和高阶隐式交叉的统一建模的 DeepFM、通过显式交叉层处理任意阶数的特征交互 DCN、聚焦于关键特征并可以对用户行为建模的 Attention 是其中的代表。

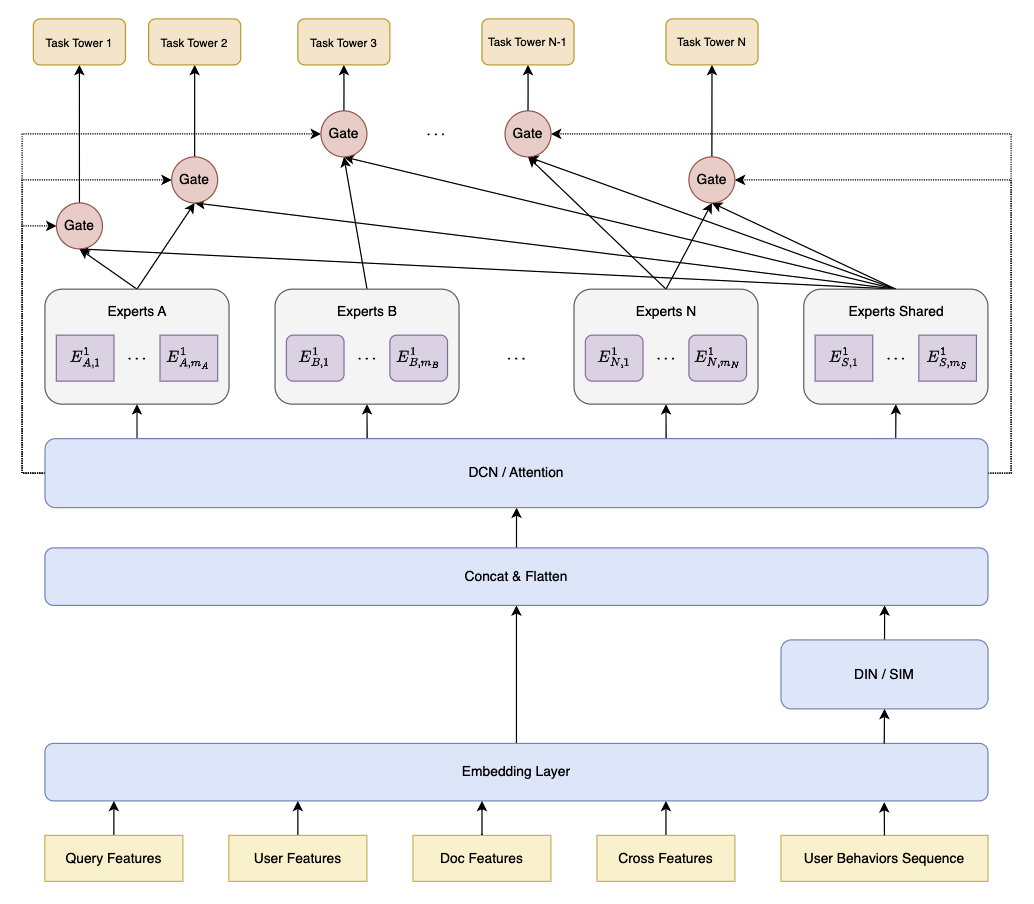
4.1、DeepFM

DeepFM 是一个结合了 FM (Factorization Machines) 和 Deep Neural Networks (DNN) 的模型，旨在通过深度学习网络和因子分解技术的结合，既能捕捉特征之间的高阶交互，又能处理大规模稀疏数据。

DeepFM的模型结构分为：

LR：基于 Logistic Regression (LR) 线性模型对特征进行建模
FM：通过因子化技术对特征之间的交互进行建模，捕捉特征的二阶交互
DNN：深度神经网络通过多层全连接网络学习更高阶的特征交互

4.1.1、LR

假设输入特征为 $(\mathbf{x} = [x_1, x_2, …, x_N]$，其中 $x_i$ 代表特征，$N$ 是特征的数量，LR可以描述为：

\[\hat{y}_{\text{LR}} = w_0 + \sum_{i=1}^{N} w_i x_i\]

其中 $w_0$ 是全局偏置项，$w_i$ 是特征 $x_i$ 的权重。

4.1.2、FM

FM部分用于捕捉特征间的二阶交互，FM模型通过将特征映射到低维因子向量来建模特征之间的交互关系。公式如下：

\[\hat{y}_{\text{FM}} = \sum_{i=1}^{N} w_i x_i + \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1, j \neq i}^{N} \langle \mathbf{v}_i, \mathbf{v}_j \rangle x_i x_j\]

$w_i$ 是每个特征的权重
$\mathbf{v}_i \in \mathbb{R}^K$ 是特征 $x_i$ 的嵌入向量（也称为因子向量），其中 $K$ 是嵌入向量的维度
$\langle \mathbf{v}_i, \mathbf{v}_j \rangle$ 表示特征 $x_i$ 和 $x_j$ 的嵌入向量之间的内积，用于建模这两个特征的交互

4.1.3、DNN

DNN部分用于学习更高阶的特征交互，通过多个全连接层来捕捉更复杂的非线性关系。公式如下：

\[\hat{y}_{\text{DNN}} = \text{DNN}(\mathbf{x})\]

其中，$\mathbf{x}$ 是输入特征向量，DNN 为多层全连接网络。

DeepFM 的最终输出是线性部分、FM部分和DNN部分的加权和：

\[\hat{y} = \alpha \cdot \hat{y}_{\text{LR}} + \beta \cdot \hat{y}_{\text{FM}} + \gamma \cdot \hat{y}_{\text{DNN}}\]

其中 $\alpha$, $\beta$, $\gamma$ 是加权系数，通常通过训练来学习。

4.2、DCN

DCN（Deep & Cross Network） 结合了 深度学习（DNN） 和 显式的特征交叉（crossing） 机制，能够有效地捕捉特征之间的高阶交互。DCN通过交叉层显式地学习特征交叉，而传统的DNN需要依靠全连接层隐式学习这些交互。DCN架构分为 Deep Network 和 Cross Network 两部分。

Cross Network 由 交叉层（Cross Layer） 构成，交叉层通过直接对输入特征进行交叉（即特征组合）来捕捉特征之间的高阶交互，不需要依赖全连接层逐层学习，从而显式建模输入特征的交互。

Cross Layer 经历了两版变化：

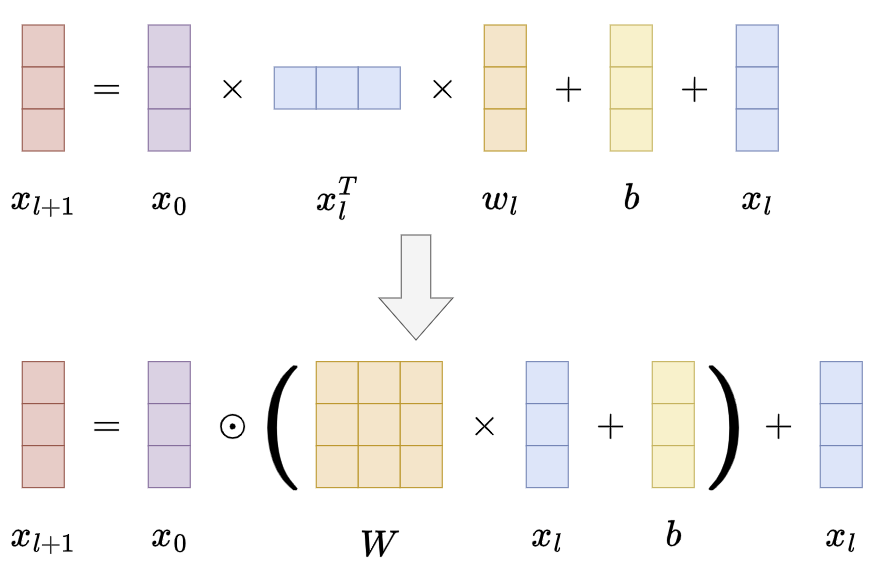
第一版：
\[{\bf x}_{l+1}={\bf x}_{0}{\bf x}_{l}^{T}{\bf w}_{l}+{\bf b}_{l}+{\bf x}_{l}=f({\bf x}_{l},{\bf w}_{l},{\bf b}_{l})+{\bf x}_{l}\]
- $x_{0} \in \mathbb{R}^{d}$ 是包含原始特征的最底层输入
- $x_{l},x_{l+1} \in \mathbb{R}^{d}$ 分别表示第 $l$ 层和第 $l+1$ 层的输出
- $w_{l},b_{l} \in \mathbb{R}^{d}$ 表示第 $l$ 层的权重矩阵和偏置参数
- 每个交叉层在特征交叉 $f$ 后都会将其输入加回，即映射函数 $f:\mathbb{R}^{d}\mapsto\mathbb{R}^{d} $ 拟合了 $x_{l+1}-x_{l}$ 的残差
第二版：
\[{\bf x}_{l+1}={\bf x_{0}}\odot(W_{l}{\bf x}_{l}+{\bf b}_{l})+{\bf x}_{l}\]
- $x_{0} \in \mathbb{R}^{d}$ 是包含原始特征的最底层输入
- $x_{l},x_{l+1} \in \mathbb{R}^{d}$ 分别表示第 $l$ 层和第 $l+1$ 层的输出
- $W_{l} \in \mathbb{R}^{d \times d}$ 和 $b_{l} \in \mathbb{R}^{d}$ 表示第 $l$ 层的权重矩阵和偏置参数
- $\odot$ 是哈达玛积运算（Hadamard Product），即逐元素相乘：两个相同大小的矩阵/向量的每个对应元素进行逐一相乘，结果仍是一个维度一致的矩阵/向量，其每个元素是原始矩阵/向量对应元素的乘积
第二版本的交叉层采用哈达玛积，向量 $w \in \mathbb{R}^{d}$ 替换为矩阵 $W \in \mathbb{R}^{d \times d}$，可以实现逐元素的加权，拟合能力加强
- 第一版的交叉层学习的是特殊类型的高阶特征交互，其中每一层都是 $x_{0}$ 的标量倍数（详细论证见xDeepFM）：
  - \[\begin{aligned} \mathbf{x}_{l+1} & =\mathbf{x}_0 \mathbf{x}_l^T \mathbf{w}_{l+1}+\mathbf{x}_l \\ & =\mathbf{x}_0\left(\left(\alpha^l \mathbf{x}_0\right)^T \mathbf{w}_{l+1}\right)+\alpha^l \mathbf{x}_0 \\ & =\alpha^{l+1} \mathbf{x}_0 \end{aligned}\]
  - 其中，
  \[\alpha^{l+1} = \alpha^{l} ({\bf x}_{0}^{T} { \bf w}_{l+1}+1 )\]
  是一个标量，因此 $x_{l+1}$ 仍然是 $x_{0}$ 的一个标量倍数

DCN还保留了DNN的设计，即通过多层全连接层（FC层）来学习输入数据的非线性表示。这部分与标准的DNN相似，通过逐层的非线性变换来提取高层次的特征。

4.3、Attention

Attention 为每个特征分配一个权重以反映该特征与其他特征之间的相对重要性。

Attention 包括：

Query（查询）：用于表示当前需要关注的目标或查询的特征
Key（键）：与Query进行匹配的特征，表示信息的内容或特征
Value（值）：与Key相关联的实际信息

Attention公式可以描述为：

\[\mathrm{Attention}(Q,K,V)=\mathrm{softmax}\!\left({\frac{Q K^{T}}{\sqrt{d_{k}}}}\right)V\]

计算步骤如下：

计算Query和Key之间的相似度Attention Score，通常使用点积（Dot-Product）或加法（Additive）计算：
\[\text{score}(Q, K) = \frac{Q K^T}{\sqrt{d_k}}\]
其中，$Q$ 是Query向量，$K$ 是Key向量，$d_k$ 是Key向量的维度，通常做缩放以防止点积过大。
将相似度分数通过Softmax函数转换为概率分布（Attention权重）：
\[\text{Attention Weight} = \text{Softmax}(\text{score}(Q, K))\]
通过加权平均Value，得到最终的输出：
\[\text{output} = \sum (\text{Attention Weight} \times V)\]

5、用户行为序列建模

精排中的 用户行为序列建模 是提升搜索系统性能的关键策略。用户行为序列指的是用户与系统之间发生的交互记录，通常按时间顺序排列，包括用户的点击、浏览、购买、收藏、评论等行为。通过对这些行为序列的建模，可以深入理解用户的兴趣演化、短期和长期偏好，进而在搜索结果排序时精准匹配用户当下的需求。

5.1、DIN

Deep Interest Network (DIN) 通过注意力机制对用户的历史行为序列进行加权，挖掘与当前候选物品/文档相关的用户行为，用于捕捉用户的动态兴趣。

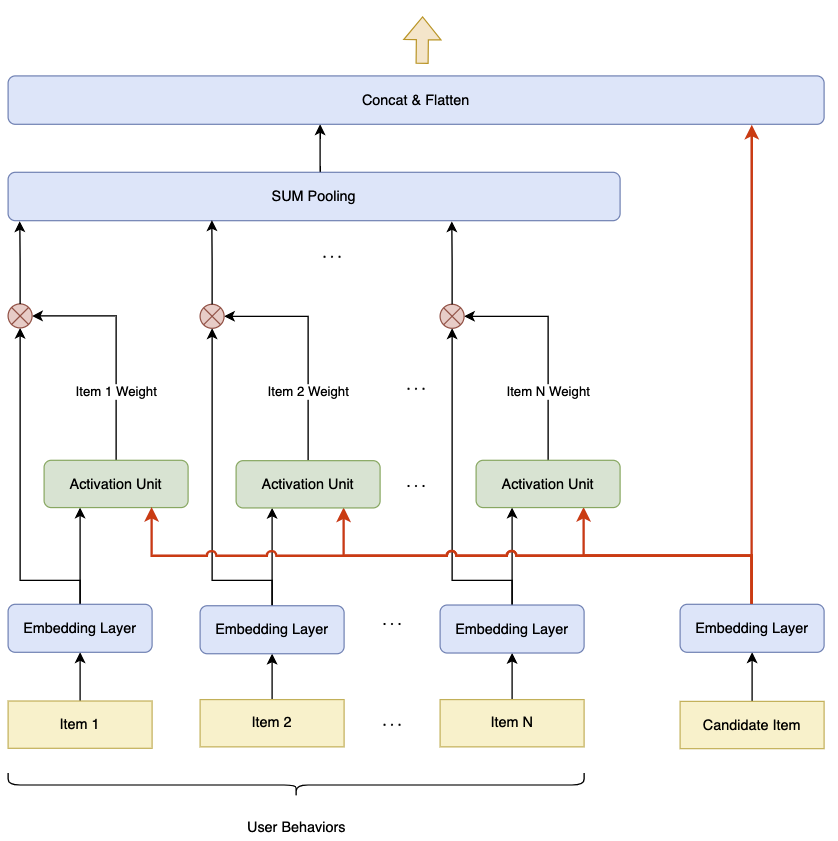
输入
- 用户行为序列 $ {x_1, x_2, \ldots, x_n} $，其中 $ x_i $ 表示用户的第 $ i $ 个历史行为的特征向量
- 候选文档/物品 $ q $ 的特征向量
- 用户和上下文特征 $ u $（如年龄、性别等）
兴趣提取
- 注意力机制：对每个历史行为 $ x_i $，计算其与候选物品 $ q $ 的相关性权重 $ \alpha_i $：
  \[\alpha_i = \frac{\exp(\text{score}(x_i, q))}{\sum_{j=1}^n \exp(\text{score}(x_j, q))}\]
  其中：
  \[\text{score}(x_i, q) = f(\mathbf{W}_1 x_i + \mathbf{W}_2 q + b)\]
  $ f $ 是非线性激活函数（如 ReLU），$ \mathbf{W}_1$，$ \mathbf{W}_2$，$ b $ 为可学习参数。
- 加权兴趣向量：将权重 $ \alpha_i $ 应用于用户行为序列，得到加权兴趣向量：
  \[\mathbf{v} = \sum_{i=1}^n \alpha_i \cdot x_i\]
特征融合

将加权兴趣向量 $ \mathbf{v} $、候选物品特征 $ q $、用户上下文特征 $ u $ 拼接成输入向量 $ z $：
\[z = [\mathbf{v}, q, u]\]
输出

通过全连接网络（MLP），计算点击概率 $ \hat{y} $：
\[\hat{y} = \sigma(\mathbf{W}_o \cdot g(z) + b_o)\]
其中 $ g $ 是 MLP 的非线性变换，$ \sigma $ 是 Sigmoid 激活函数。
损失函数

使用二分类的交叉熵损失：
\[\mathcal{L} = - \frac{1}{N} \sum_{i=1}^N \left[ y_i \log(\hat{y}_i) + (1 - y_i) \log(1 - \hat{y}_i) \right]\]
其中 $ y_i $ 为真实点击标签。

5.2、SIM

Search-based Interest Model（SIM）针对用户超长行为序列的建模框架，主要分为两大关键组件：泛搜单元（GSU, General Search Unit）和精搜单元（ESU, Exact Search Unit）。

5.2.1、GSU

GSU 的主要目标是从用户的超长行为序列中进行粗粒度搜索，以提取出与候选物品有潜在相关性的行为子序列（Sub-Behavior Sequence, SBS）。GSU 将大量无关行为过滤掉，从而大幅降低后续精细建模的计算开销。

5.2.1.1、硬搜索

硬搜索基于规则或简单的匹配策略对用户行为序列 $ H $ 进行筛选，快速选出与候选文档/物品相关的子序列 $ H’ $。

\[H'_{\text{hard}} = \{h_i \mid \text{rule}(h_i, c)\}\]

$ H = {h_1, h_2, \ldots, h_T} $ 为用户超长行为序列
$ c $ 为候选文档/物品，当前需要预测用户行为的目标文档/物品
典型规则：
- 类目匹配：$ \text{category}(h_i) = \text{category}(c) $
- 时间窗口：只选择行为时间在最近 $ N $ 天内的记录
- 滑窗机制：截取序列中的固定窗口长度

5.1.1.2、软搜索

软搜索通过轻量级模型评估每个行为与候选文档/物品的相关性，并筛选出得分较高的行为。

\[H'_{\text{soft}} = \{h_i \mid \text{score}(h_i, c) > \theta\}\]

相关性得分公式：
\[\text{score}(h_i, c) = f_{\text{sim}}(x_i, x_c) + f_\text{time decay}(h_i, c)\]
- $ f_{\text{sim}} $：基于向量的相似度函数（如内积、余弦相似度）
- $ f_\text{time decay} $：时间衰减函数，优先选择最近的行为

5.1.2、ESU

ESU 对 $ H’ $ 进行深度建模，捕捉行为与候选文档/物品之间的高阶交互关系。

5.1.2.1、注意力机制

ESU 利用注意力机制评估每个行为的重要性，生成加权特征表示。

\[\alpha_i = \frac{\exp(f_a(x_i, x_c))}{\sum_{h_j \in H'} \exp(f_a(x_j, x_c))}\]

$ x_i \in \mathbb{R}^d $：行为 $ h_i $ 的特征表示
$ x_c \in \mathbb{R}^d $：候选物品的特征表示
$ f_a(x_i, x_c) $：注意力得分函数（如 MLP）
$ \alpha_i $：表示行为 $ h_i $ 的权重

5.1.2.2、特征聚合

利用加权机制提取长期兴趣序列特征 $ l $：

\[l = \sum_{h_i \in H'} \alpha_i \cdot x_i\]

5.1.2.3、评分与排序

结合用户短期兴趣特征 $ s $、候选物品特征 $ x_c $ 和长期兴趣序列特征 $ l $，计算最终的兴趣得分：

\[s = g([s; x_c; l])\]

其中，$ g $ 是多层感知机（MLP）或其他评分函数。

6、多目标预估

对于搜索平台而言，存在多个重要的业务目标需要兼顾。除了提高用户的点击率和转化率以增加平台收益外，还需考虑用户的满意度、留存率、活跃度等，以实现平台的长期可持续发展。

多目标预估可以在模型训练和优化过程中，合理权衡这些不同业务目标之间的关系，避免过度追求某一目标而损害其他目标，使平台在短期收益和长期发展之间找到平衡。

搜索常见的目标包括点击、点赞、收藏、评论、关注、分享、截图等。在多目标建模中，通常采用共享底层网络，多个目标在同一个深度学习模型中共享一部分参数，同时在上层使用独立的任务头进行优化。经过业界的实践，ESSM、ESCM、MMoE、PLE等是应用广泛的模型。

6.1、Share Bottom

Share Bottom 是最直接简单的多任务学习（Multi-Task Learning, MTL）模型架构，其基本思想是通过共享底层特征提取层，让不同任务能够共同利用底层特征，从而提升模型的学习能力。

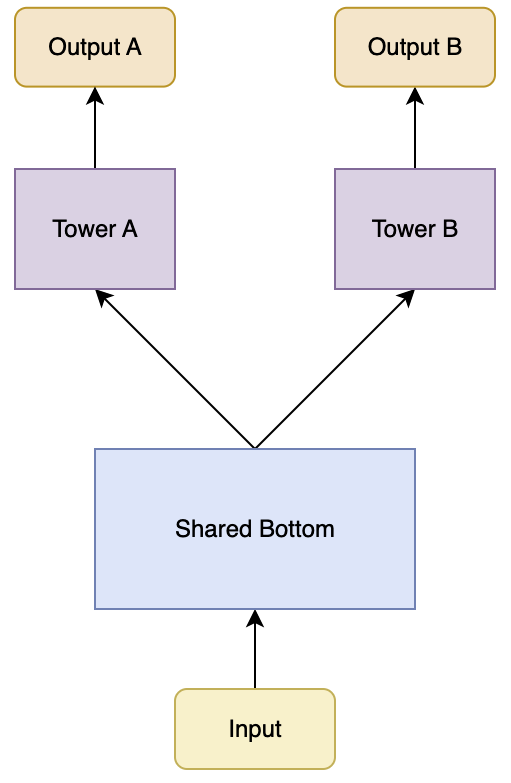
负迁移问题
- 当多个任务之间的差异较大，而共享底层网络层过于简单或固定时，可能会出现负迁移现象。即一个任务的学习过程对另一个任务产生负面影响，导致模型在某些任务上的性能下降。模型无法区分不同任务的特定需求，容易导致任务间的冲突
任务不平衡问题
- 如果不同任务的数据分布、难易程度或重要性存在较大差异，模型在训练过程中可能会倾向于优化表现较好或数据量较大的任务，导致模型在某些任务的稀疏样本上表现较差，并容易对部分任务过拟合

6.2、MMoE

MMoE（Multi-gate Mixture of Experts） 通过为每个任务构建专属的专家网络，并利用共享网关机制来动态选择不同任务最适合的专家，从而实现有效的任务协同。

任务 $ T_k $ 的最终输出由多个共享专家网络 $(e_1, e_2, \dots, e_N)$ 的加权组合生成，权重由任务特定的门控网络 $g_k$ 动态计算。

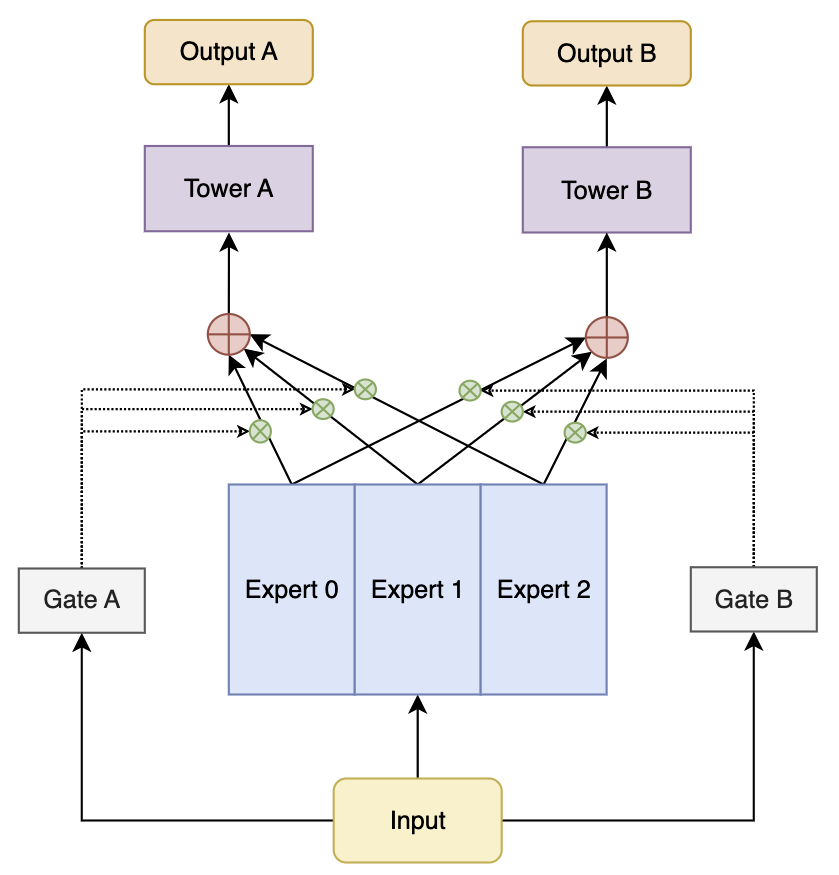
6.2.1、专家网络

每个专家网络的输入为通用特征 $ x $，经过专家网络 $e_i$ 后得到输出 $h_i$：

\[h_i = e_i(x), \quad i = 1, 2, \dots, N\]

其中：

$ e_i $ 是第 $ i $ 个专家网络
$ h_i \in \mathbb{R}^d $ 是第 $ i $ 个专家网络的输出

6.2.2、门控网络

任务 $ T_k $ 的门控网络根据输入特征 $ x $，计算每个专家的权重 $ g_{k,i} $：

\[g_{k,i} = \text{softmax}\left(W_k \cdot x + b_k\right)_i\]

其中：

$ g_{k,i} \in [0, 1] $ 是专家 $ e_i $ 对任务 $ T_k $ 的权重
$ W_k $ 和 $ b_k $ 是门控网络的参数

6.2.3、专家输出融合

任务 $ T_k $ 的最终共享特征输出 $ o_k $ 是所有专家输出的加权和：

\[o_k = \sum_{i=1}^N g_{k,i} \cdot h_i\]

其中：

$ g_{k,i} $ 是任务 $ T_k $ 对专家 $ e_i $ 的权重
$ h_i $ 是专家 $ e_i $ 的输出

6.2.4、任务预测

共享特征 $ o_k $ 传递到任务特定的预测网络 $ f_k $，得到最终的任务预测结果：

\[\hat{y}_k = f_k(o_k)\]

其中 $ f_k $ 是任务 $ T_k $ 的特定网络。

6.3、PLE

Progressive Layered Extraction (PLE) 通过引入渐进式分层提取策略，在共享和特定任务之间有效分离参数和信息，解决多任务间的负迁移和跷跷板现象（即不同任务难以同时优化的问题）。

MMoE 核心设计基于共享底层专家（Experts）和动态门控网络（Gate），相比于 MMoE，PLE 增加了：

任务独占专家（Task-specific Experts）：共享专家网络负责提取任务之间的共享信息，而任务独占专家网络则负责提取任务特定的信息
多层渐进提取机制：包含多个层级的专家网络和门控网络，每个层级的专家网络专注于学习不同层次的特征表示。在底层，专家网络学习较为通用的特征，随着层级的上升，专家网络逐渐学习到更任务特定的特征

PLE 通过上述设计有效缓解了如下问题：

负迁移（negative transfer）： 当任务之间相关性较弱时，共享参数反而导致模型性能下降，PLE 通过任务间共享模块和任务特定模块的有效分离，减少任务间冲突
跷跷板现象（seesaw phenomenon）： 指一个任务的性能提升往往以牺牲另一个任务的性能为代价，PLE 多层提取机制逐步增强不同任务的表现，同时保持整体性能稳定

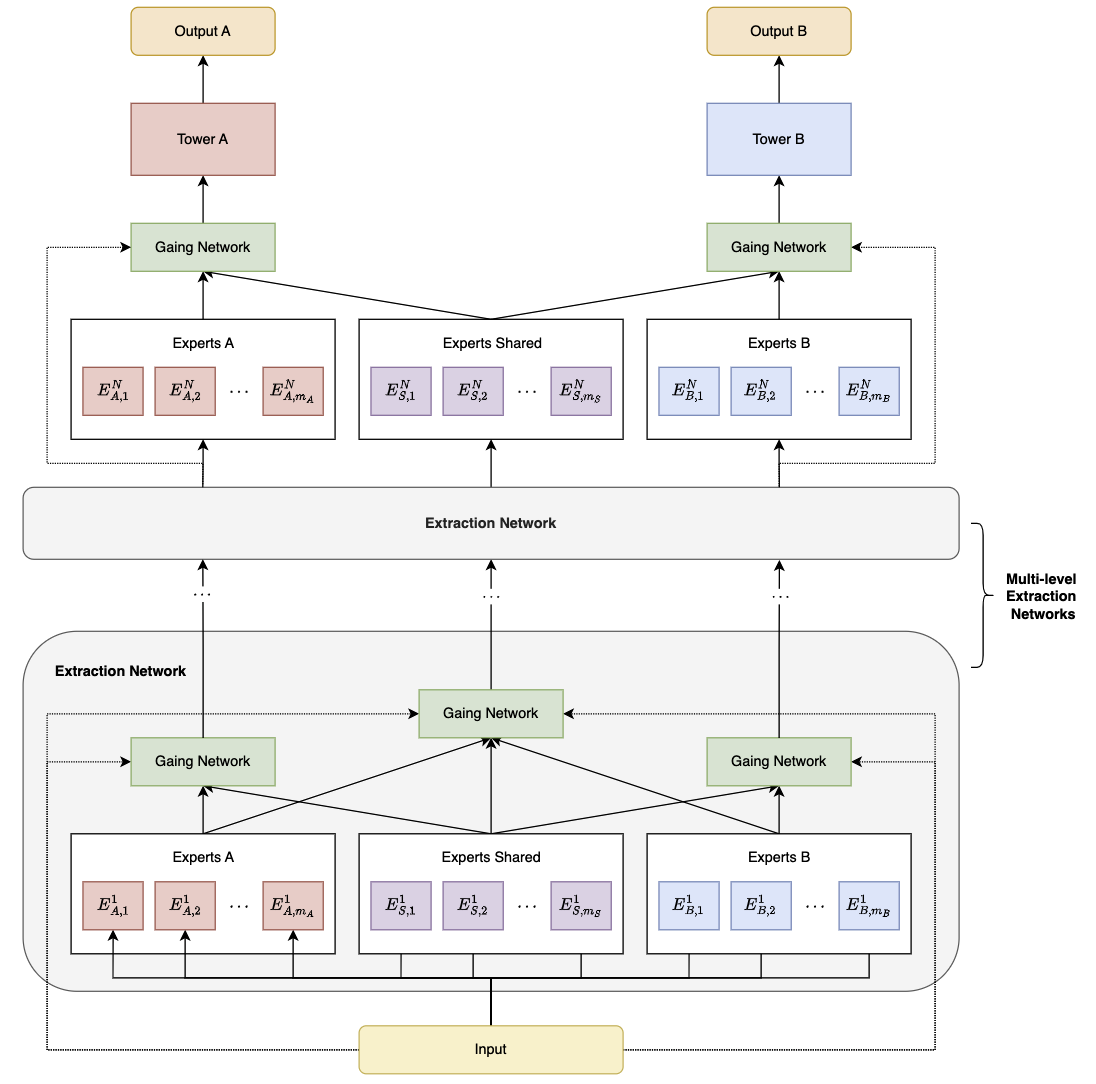
如图，Experts A 和 Experts B 为任务 A 和任务 B 的独占专家系统，Experts Shared 为共享专家系统，Gating Network 为门控网络，每个任务采用独占专家和共享专家中的多个 Expert。

任务 $k$ 的门控网络输出公式为：

\[g^{k}\left(x\right)=w^{k}\left(x\right)S^{k}\left(x\right)\]

其中，$x$ 为输入表示，$w^{k}$ 为加权函数以表示专家系统 $S^{k}$ 中 Experts 的权重：

\[w^{k}(x)=\operatorname{Softmax}(W_{g}^{k}x)\]

其中，$W_{g}^{k}\in R^{(m_{k}+m_{s})\times d}$ 为参数矩阵，$m_{s}$ 和 $m_{k}$ 分别是共享专家和任务 $k$ 的特定专家的数量，$d$ 是输入表示的维度。$S^{k}$ 由共享专家和任务 $k$ 的独占专家组成：

\[S^{k}(x)=[E_{(k,1)}^{T},E_{(k,2)}^{T},\cdots,E_{(k,m_{k})}^{T},E_{(s,1)}^{T},E_{(s,2)}^{T},\cdots,E_{(s,m_{s})}^{T}]^{T}\]

即，任务 $k$ 的预测输出为：

\[y^{k}(x)=t^{k}(g^{k}(x))\]

其中 $t_{k}$ 表示任务 $k$ 的塔网络（tower network），$g_{k}$ 如上所述为任务 $k$ 的门控网络（gating network）。

7、多目标融合

多目标预估会对每个目标预测一个分数，在文档排序时需要综合多个目标打分，即采用多目标融合将多个优化目标（点击率、转化率、相关性、停留时长、点赞率、收藏率、分享率、评论率、关注率、质量分等）综合在单一评分框架中，从而实现对文档的统一排序，平衡用户体验和业务指标。

7.1、融合公式

7.1.1、加法融合

加法融合是最简单的一种方式，将各目标的分数按权重线性加权求和，生成最终分数，适合目标分数量级一致的情况。

设有 $ n $ 个目标，每个目标的得分为 $ S_i $，对应的权重为 $ w_i $（满足 $ \sum_{i=1}^n w_i = 1 $），则最终得分 $ S_{\text{final}} $ 定义为：

\[S_{\text{final}} = \sum_{i=1}^n w_i S_i\]

7.1.2、乘法融合

乘法融合通过乘积的方式将各目标得分结合，通常用于强调目标之间的相互增强效果，适合目标之间具有非线性放大或削弱关系的情况。

\[S_{\text{final}} = \prod_{i=1}^n S_i^{w_i}\]

等价于加权几何平均：

\[S_{\text{final}} = \exp\left(\frac{1}{\sum_{i=1}^n w_i} \sum_{i=1}^n w_i \ln S_i \right)\]

7.1.3、带权指数融合

带权指数融合通过对目标分数进行指数放大后加权，增强高分目标的影响力，适合目标分数分布差异较大、需要增强高分贡献的场景。

\[S_{\text{final}} = \sum_{i=1}^T (\alpha_i + w_i S_i)^{\beta_i}\]

其中，$\alpha_i$ 为目标偏置，$\beta_i$ 是调整目标权重的指数参数，用于非线性处理。

7.1.4、基于排名的融合

当目标分布不稳定时，基于排名的融合方法通过对每个目标的得分排序，按排名进行融合，只关注文档在各目标中的相对顺序，避免目标分数尺度不一致的影响。

设目标 $ i $ 的分数对应排名为 $ R_i $，则最终得分定义为：

\[S_{\text{final}} = \sum_{i=1}^n w_i \cdot f(R_i)\]

其中：

$ R_i $ 是目标 $ i $ 的排名（如第 $ R_i $ 名得分）。
$ f(\cdot) $ 是排名到分数的映射函数，如 $ f(R) = 1/R $ 或 $ f(R) = e^{-R} $。
$ w_i $ 是权重。

另一种实现是基于排名的加权投票：

\[S_{\text{final}} = \sum_{i=1}^n w_i \cdot \mathbb{I}(R_i \leq k)\]

其中 $ \mathbb{I} $ 是指示函数，表示目标 $ i $ 的排名是否在前 $ k $ 名。

7.1.5、目标分预处理

在排序融合公式中，预处理目标分的步骤是关键环节，特别是在目标分分布不均或不稳定时，通过特定的变换处理，可以显著提高排序性能。

7.1.5.1、Min-Max 归一化

归一化用于将目标分映射到指定的范围（通常是 [0,1] 或 [-1,1]），以消除不同目标分之间的量纲差异，确保它们在同一尺度上，便对不同尺度的目标分进行统一处理：

\[x' = \frac{x - \min(x)}{\max(x) - \min(x)}\]

扩展到任意范围 $[a, b]$: $x' = a + \frac{(x - \min(x)) \cdot (b - a)}{\max(x) - \min(x)}$

7.2、搜参算法

7.2.1、贝叶斯优化

贝叶斯优化（Bayesian Optimization）是一种基于贝叶斯统计方法的全局优化算法，适用于黑盒函数优化问题。贝叶斯调参能够利用历史的评估结果，通过构建目标函数的概率模型，选取具有最大潜在收益的参数点进行评估，从而以较少的迭代次数找到最优参数。具体步骤如下：

定义目标函数：定义目标函数 $f(x)$ （$x$ 是超参数）用于评估召回合并策略的效果
\[f(\mathbf{w})=\mathbf{Metric}(\mathbf{Merge}(\mathrm{Recalls}(\mathbf{w})))\]
- $\text{Recalls}(\mathbf{w}) = [R_1(w_1), R_2(w_2), \dots, R_n(w_n)]$ 表示来自不同通道的召回结果，每个 $R_i(w_i)$ 是通道 $i$ 根据权重 $w_i$ 所返回的候选集
- $\text{Merge}(\cdot)$ 表示将各个通道的召回结果按权重加权融合
- $\text{Metric}(\cdot)$ 是根据合并后的候选集评估的性能指标
设置参数空间：如果使用加权平均的合并方式，可以将每个通道的权重作为调节参数进行优化
- 比如，设定权重参数 $\mathbf{w}=[w_{1},w_{2},\cdot\cdot\cdot,w_{n}]$，每个召回通道的权重 $w_{i}$ 影响候选项排名和选择
\[{\bf w}=[w_{1},w_{2},\cdot\cdot\cdot,w_{n}]\;\;\;\;\mathrm{with}\;\;\;\;\sum_{i=1}^{n}w_{i}=1,\;\;\;\;w_{i}\in[0,1]\]
初始化高斯过程：为待优化的参数空间设定先验分布，通常使用高斯过程（Gaussian Process, GP）作为先验，表示对参数空间的初步认识
\[p(f(\mathbf{w}))\sim{\mathcal{G P}}(m(\mathbf{w}),k(\mathbf{w},\mathbf{w}^{\prime}))\]
- 其中 $m(\mathbf{w})$ 是目标函数的均值函数，通常假设为零；$ k(\mathbf{w}, \mathbf{w}’) $ 是协方差函数，用于表示不同参数配置之间的相似性
更新后验分布：在每次迭代中，根据当前的参数空间和目标函数值，更新高斯过程的后验分布，并基于当前的后验分布生成新的参数选择。贝叶斯调参使用获取函数（Acquisition Function）来选择下一个要评估的参数点。常见的获取函数如期望改进（Expected Improvement, EI）
\[\alpha(\mathbf{w}) = \mathbb{E}[ \Delta f(\mathbf{w}) ] = \mathbb{E}[ \max(0, f(\mathbf{w}_{\text{best}}) - f(\mathbf{w})) ]\]
- $f(\mathbf{w}_{\text{best}})$ 是当前最好的目标函数值
- $\Delta f(\mathbf{w})$ 是期望的改进
选择下一个评估点：通过最大化获取函数来决定下一个评估点。获取函数根据当前的后验分布选择一个最有可能提升目标函数值的参数组合，从而进行下一轮评估
\[\mathbf{w}^*=\arg \max _{\mathbf{w}} \alpha(\mathbf{w})\]
重复迭代：贝叶斯优化会根据每一轮评估的结果，调整先验分布，不断优化目标函数，最终找到全局最优的参数配置
\[p(f(\mathbf{w})\mid\mathbf{w}^{*},f(\mathbf{w}^{*}))\sim{\mathcal{G}}{\mathcal{P}}({\mu}(\mathbf{w}),\Sigma(\mathbf{w}))\]

最终，贝叶斯优化会返回最优的参数 $\mathbf{w}^*$。

7.3、模型融合

7.3.1、LTR 建模

采用学习排序（Learning to Rank, LTR）建模融合分的方式，是通过模型将多目标预估分数结合用户、查询、文档特征转化为最终排序分数的过程。

LTR 的目标是优化一个排序函数 $ f $，使得对于一个查询 $ q $，能对候选文档列表 $ D $ 排出最佳顺序。

输入：查询 $ q $、文档特征 $ x_i $ 和初始目标预估分数 $ s_i $。
输出：排序得分 $ y_i = f(x_i, s_i) $。

不同 LTR 方法定义的损失函数不同，具体可分为 Pointwise、Pairwise、Listwise。

7.3.1.1、Pointwise Loss

Pointwise Loss 只关注单个候选项（如分类或回归任务）。

均方差（Mean-Square Error，MSE）
- 定义：将排序问题视为预测相关性分数 $ \hat{y}_i $，并与真实相关性标签 $ y_i $ 之间最小化误差。
\[L_{\text{MSE}} = \frac{1}{N} \sum_{i=1}^{N} (y_i - \hat{y}_i)^2\]
- $ y_i $：第 $ i $ 个样本的真实标签（评分）
- $ \hat{y}_i $：模型预测分数
交叉熵（Cross Entropy，CE）
- 定义：将LTR的最终目标定义为分类任务，输出结果为某个互动行为的概率。分类任务采用交叉熵损失，交叉熵主要用于衡量两个概率分布之间的差异：
\[\mathrm{CE}(y,{\hat{y}})=-\sum_{i=1}^{C}y_{i}\cdot\log({\hat{y}}_{i})\]
- $y_{i}$ 是真实标签的独热编码向量，第 $i$ 类的标签为 1，其它类别为 0
- - $\hat{y}_{i}$ 是模型对于第 $i$ 类的预测概率

7.3.1.2、Pairwise Loss

Pairwise Loss 关注候选项之间的两两比较。

对比损失
- 定义：对比损失衡量两个文档的相对排序是否正确。如果文档对的相关性排序是正确的，那么损失应该较小；如果排序不正确，则损失应该较大：
\[\mathcal{L}_{\text{contrastive}} = \frac{1}{2} \left[ y \cdot d^2 + (1 - y) \cdot \max(0, m - d)^2 \right]\]
- $ y $ 是文档对的标签，取值为 0 或 1，表示文档 $ D_1$ 是否应该排在文档 $ D_2$ 之前
- $ d $ 是文档 $ D_1$ 和 $ D_2$ 在模型预测中的距离（通常是两者的评分差）
- $ m $ 是一个超参数，表示 “margin”（边际），即在没有损失的情况下，文档的评分差需要达到的最小值
RankNet损失
- 定义：RankNet 使用 对数损失 来训练排序模型。RankNet 通过概率的形式预测文档的相对排序，给定一对文档 $ D_1$ 和 $ D_2$ ，模型输出一个概率，表示 $ D_1$ 比 $ D_2$ 相关的概率：
\[\mathcal{L}_{\text{RankNet}} = - \sum_{i,j} \left[ p_{ij} \log \hat{p}_{ij} + (1 - p_{ij}) \log (1 - \hat{p}_{ij}) \right]\]
- $ p_{ij}$ 是文档对 $ D_1$ 和 $ D_2$ 的真实排序标签（如果 $ D_1$ 应该排在 $ D_2$ 前面，则 $ p_{ij} = 1$ ，否则为 0）
- $ \hat{p}_{ij}$ 是模型预测 $ D_1$ 排在 $ D_2$ 前面的概率

7.3.1.3、Listwise Loss

Listwise Loss 直接优化一个完整候选列表的排名质量。

LambdaRank
- 定义：LambdaRank 在 RankNet 的基础上进一步发展，旨在直接优化排序指标（如 NDCG）而设计。
- 目标函数： LambdaRank 的核心在于设计与排名指标相关的动态梯度权重，以高效优化目标。
  - NDCG 指标
    \[\text{NDCG@k} = \frac{\sum_{i=1}^k \frac{2^{y_i} - 1}{\log_2(i + 1)}}{\text{IDCG@k}}\]
    - $ y_i $：文档 $ i $ 的相关性标签（通常是人工标注或规则确定的相关性得分）
    - $ i $：文档在当前排序中的位置
    - $ \text{IDCG@k} $：理想情况下的 DCG 值（Ideal DCG）
  - 梯度
    - 定义：对于候选文档对 $ (i, j) $，假设 $ y_i > y_j $（即文档 $ i $ 比 $ j $ 更相关），对应的梯度更新为：
    \[\lambda_{ij} = \left| \Delta Z_{ij} \right| \cdot \sigma(s_j - s_i)\]
    - $ \Delta Z_{ij} $：交换文档 $ i $ 和 $ j $ 后，排名指标（如 NDCG）的增量变化 $\Delta Z_{ij} = \left| \frac{1}{\log_2(1 + \text{rank}_i)} - \frac{1}{\log_2(1 + \text{rank}_j)} \right| \cdot \left| 2^{y_i} - 2^{y_j} \right|$
    - $ \sigma(s_j - s_i) $：模型预测的分数差对应的 Sigmoid 函数 $\sigma(s_j - s_i) = \frac{1}{1 + \exp(s_i - s_j)}$
- 损失函数：LambdaRank 的损失函数是基于梯度权重的更新，而不是显式地定义为一个封闭公式。但可以通过梯度描述模型的优化方向：
  \[\mathcal{L}_{\text{LambdaRank}} = \sum_{i,j} \lambda_{ij} \cdot \log(\sigma(s_i - s_j))\]
- 梯度更新：对文档 $ i $ 的得分 $ s_i $ 的梯度更新规则为：
  \[\frac{\partial \mathcal{L}}{\partial s_i} = \sum_{j \neq i} (\lambda_{ij} - \lambda_{ji})\]
  - 如果 $ y_i > y_j $，则 $ \lambda_{ij} > 0 $，模型需要提升 $ s_i $
  - 如果 $ y_i < y_j $，则 $ \lambda_{ij} < 0 $，模型需要降低 $ s_i $

8、总结

精排需要从粗排的候选集中进一步筛选并精细化排序，确保最相关的文档排在最前面。精排模型通常需要复杂的特征输入和先进的模型结构来处理深层的语义和行为信息。在精排策略的设计上需要重点关注以下几个方面：

特征交叉与深度特征学习
- Query、用户、文档的特征交互
- 用户兴趣的长短期交叉
- 上下文特征与文档特征的交叉
用户序列特征的应用
- 根据用户行为序列捕捉用户兴趣的演化
- 根据用户的实时行为动态调整排序策略
多目标优化与业务指标的平衡
- 联合训练多个目标
精排与粗排的协同优化
- 目标一致性
- 特征共享与传递
- 粗排和精排在计算效率和精度之间的互相权衡

参考文献

Embedding-based Retrieval in Facebook Search
Embedding-based Product Retrieval in Taobao Search
Multi-Objective Personalized Product Retrieval in Taobao Search
MOBIUS: Towards the Next Generation of Query-Ad Matching in Baidu’s Sponsored Search
FiBiNET: Combining Feature Importance and Bilinear feature Interaction for Click-Through Rate Prediction
Dense Text Retrieval based on Pretrained Language Models: A Survey
Deep Interest Network for Click-Through Rate Prediction
xDeepFM: Combining Explicit and Implicit Feature Interactions for Recommender Systems
Deep & Cross Network for Ad Click Predictions
DCN V2: Improved Deep & Cross Network and Practical Lessons for Web-scale Learning to Rank Systems
Squeeze-and-Excitation Networks
Notes on Noise Contrastive Estimation and Negative Sampling
Learning Tree-based Deep Model for Recommender Systems
Approximate Nearest Neighbor Search under Neural Similarity Metric for Large-Scale Recommendation
Beyond Two-Tower Matching: Learning Sparse Retrievable Cross-Interactions for Recommendation
Deep Retrieval: An End-to-End Learnable Structure Model for Large-Scale Recommendations
$I^3$ Retriever: Incorporating Implicit Interaction in Pre-trained Language Models for Passage Retrieva
A Dual Augmented Two-tower Model for Online Large-scale Recommendation
Multivariate Representation Learning for Information Retrieval
Beyond Two-Tower: Attribute Guided Representation Learning for Candidate Retrieval
Multi-Aspect Dense Retrieval
VIRT: Improving Representation-based Text Matching via Virtual Interaction
Modeling Task Relationships in Multi-task Learning with Multi-gate Mixture-of-Experts
Progressive Layered Extraction (PLE): A Novel Multi-Task Learning (MTL) Model for Personalized Recommendations